Cutting A Scaled Cone
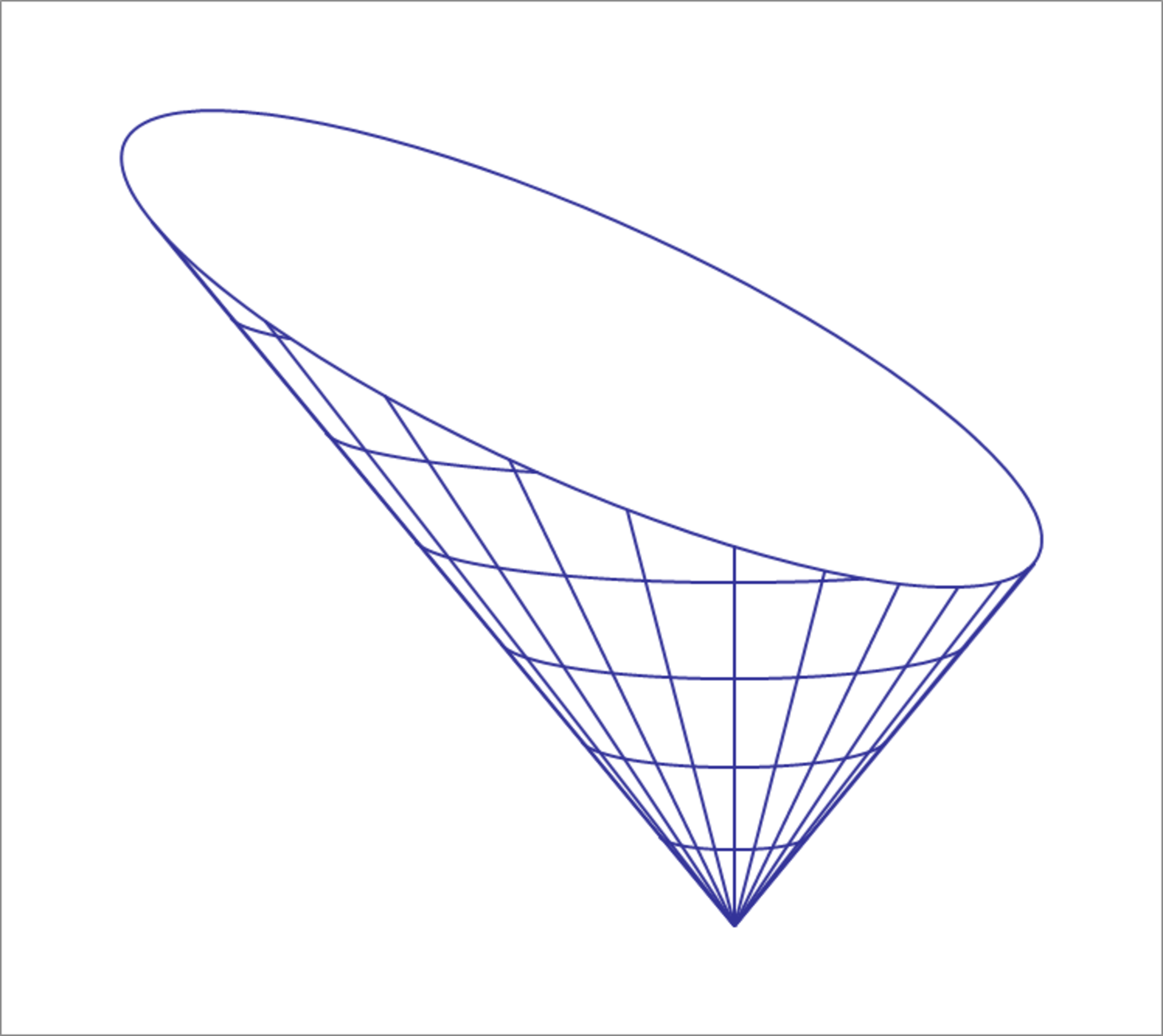
A cone with vertex at the origin and opening upward, with axis along the positive -axis, is scaled (stretched) along the -axis direction by a factor of 2. The angle between the surface of the unstretched cone and its axis, is . A plane with equation cuts though this stretched cone. The intersection between the plane and the stretched cone is an ellipse. Find the sum of the semi-minor and semi-major axes of this ellipse.
Round your answer to three decimal places.
The answer is 64.733.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Equation of regular cone, with angle θ c between its surface and its axis, is:
r ⋅ k ^ = cos θ c ∣ r ∣
Let r' be the corresponding point on the stretched cone, then
r ′ = S r
where
S = ⎣ ⎡ S x 0 0 0 S y 0 0 0 S z ⎦ ⎤
Thus r = S − 1 r ′
Thus for a stretched cone, its equation is obtained by replacing the vector r with S − 1 r ′ ,
So, we have,
( ( S − 1 r ′ ) . k ) 2 = cos 2 θ c ( S − 1 r ′ ) ⋅ ( S − 1 r ′ )
hence the equation becomes
r T Q r = 0
where
Q = S − 1 ( k k T − cos 2 θ c I ) S − 1
at the final step, I replaced r ′ with r , for notation simplicity.
Now, the equation of the cutting plane in vector form is r = r 0 + V u , where V = [ v 1 , v 2 ] , where v 1 , v 2 are two unit vectors that are orthogonal to each other and to the normal to the plane. u is the coordinate vector with respect to v 1 and v 2 .
Substituting this into the equation of the stretched cone,
( r 0 + V u ) T Q ( r 0 + V u ) = 0
Expanding
u T V T Q V u + 2 r 0 T Q V u = − r 0 T Q r 0
the left hand side can be rewritten as
( u − u 0 ) T V T Q V ( u − u 0 ) − u 0 T V T Q V u 0
where u 0 = − ( V T Q V ) − 1 V T Q r 0
Hence,
( u − u 0 ) T V T Q V ( u − u 0 ) = u 0 T V T Q V u 0 − r 0 T Q r 0
Define A = V T Q V and c = u 0 T V T Q V u 0 − r 0 T Q r 0 , then we have
( u − u 0 ) T A ( u − u 0 ) = c
Dividing both sides by c,
( u − u 0 ) T B ( u − u 0 ) = 1
where B = A / c
Since B is symmetric, we can find a rotation matrix (an orthogonal matrix) R and a diagonal matrix D, such that
R T B R = D
Note that
R = [ cos θ sin θ − sin θ cos θ ]
This suggests the change of variable, u = u 0 + R w , that leads to the simpified expression
w T D w = 1
Thus with respect to the w-coordinate frame, this is an ellipse with semi-major and semi-minor axes equal to the reciprocal of the square roots of the diagonal elements of D.
Note that since u and w are related by a translation and a rotation then these dimensions remain unchanged when moving from the w-coordinates to the u-coordinates.
In particular, since u = u 0 + R w , and since R is a rotation matrix by an angle θ , then with respect to the u-coordinate frame, this is an ellipse centered at u_0, with its axes rotated by the angle θ .
And finally, r = r 0 + V u = r 0 + V ( u 0 + R w ) = r 0 + V u 0 + V R w
Therefore, r describes an ellipse centered at r 0 + V u 0 , having its major and minor axes in the plane spanned by { v 1 , v 2 } , rotated by angle θ from the direction of v 1 and v 2 .
Making the necessary calculations, we obtain a semi-minor axis of m = 2 0 . 7 0 2 7 6 and a semi-major axis of M = 4 4 . 0 2 9 8 4 8 , making the answer M + m = 6 4 . 7 3 3