Cutting a square

Relevant wiki: Rectangle

First note that the square cannot be cut into 3 rectangles with a perimeter of 2. If it were possible one of the rectangles would have to contain two corners of the original square. If these corners were opposite corners of the square then this rectangle would be the whole square so these corners must be adjacent and so one of the edges of the rectangle would need to have length 1, a contradiction as this edge along with its opposite edge give a combined length of 2 and so its perimeter is strictly greater than 2.

For 5,6 and 7 rectangles we give a possible construction of such a cut.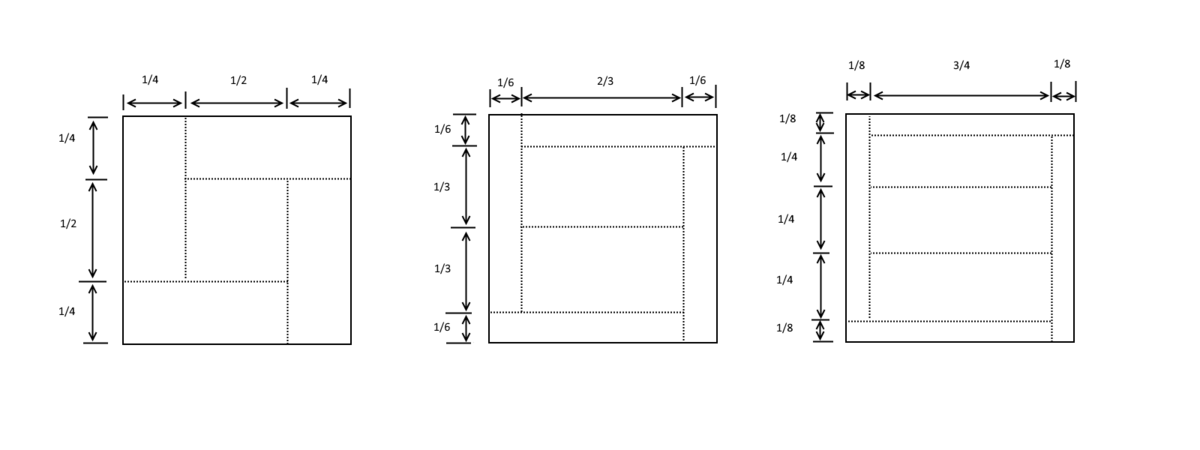

Following the pattern above we can generalise this construction to cut out $k \ge 4$ rectangles from a unit square, each with perimeter 2. The outer 4 rectangles will have a size: $\frac{1}{2k - 6}$ by $\frac{2k - 7}{2k - 6}$ and for $k > 4$ the inner rectangles will have a size: $\frac{1}{k-3}$ by $\frac{k-4}{k-3}$ .

Relevant wiki: Perimeter

I will simply prove that three is impossible.

The unit square has perimeter $4$ . Every "cut" made inside the unit square is the boundary of two smaller rectangles. If the total length of all cuts is $c$ , then the sum of the perimeters of the smaller rectangles is $\sum P = 4 + 2c.$ In the case of three rectangles, $\sum P = 3\times 2 = 6$ . This implies $c = \frac{\sum P - 4}2 = \frac{6-4}2 = 1.$ However, if we cut the square into three rectangles, one rectangle must have unit height; this already requires a cut of length one. We have nothing to spare for a second cut to create the third rectangle.

cut this square into 2 rectangles will let the sum of perimeter becomes 6, so 3 rectangles with a perimeter 2 is impossible

ITs Impossible that a square can be cut to 3 rectangles