Cutting an Annulus
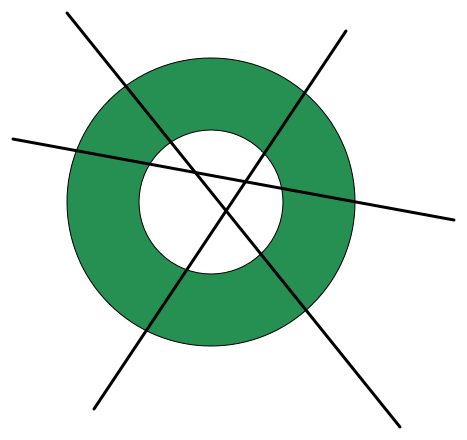What is the maximum number of pieces into which a ring can be cut by 3 straight lines?
In the image above, the ring is cut into 6 pieces by 3 lines.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Why is this the maximum?
Log in to reply
an annulus has a inner and outer circle. and we know that the maximum regions that 3 lines can make in a circle is 7. the region between three line's intersection is a triangle. so if the inner circle of annulus touch/cut each 2 sides of triangle - not the extensions of its sides-, there will be 3 more regions and -1 region (-1 is for the part of triangle which is in the inner circle) for the annulus. and by giving an example it can be proved. for the general case, (((((MAYBE))))) if we can prove that there exists n lines which cut outer circle to the most regions, and up to n intersections of n lines (that n inter sections, must be the innest ones!), make a convex polygon (with n sides), and the inner circle can be drawn somehow, cutting each side of the polygon, the most regions will be: the most regions can n lines make in a circle + n -1. for example with 4 lines: 11 + 4 - 1 = 14 regions or with 5 lines: 16 + 5 - 1 = 20 regions
Log in to reply
Great! Could you add that explanation into the solution?
I'm more iffy with the general case, because I don't immediately see how to get "lines to cut the inner circle" + "avoid having regions contained in the inner circle". I believe it is possible, but haven't worked out the details of it.
A ring is a three dimensional object. By using one line to cut the ring into two rings and two more cuts to turn each smaller ring into 5 pieces, you can get 10 pieces with three cuts.
Log in to reply
If you were looking at the 3-d analogue of this problem, then the answer (for 3 cuts) is 14.
This is much more correct - an annulus is the area between two concentric circles. but the question is for a ring! nowhere does it mention two dimensional! actualy it doesn't mention number of dimensions at all!!!!! one thing for sure is the answer is higher than the maximum 9 offered - so it is wrong period - a bad question indeed. I suggest you rethink this completely
It's a bad question. It says a "ring" not an annulus. You can only get 6 from a ring.
Log in to reply
What's the difference between a (2-d) ring and an annulus? IE Why can't we cut as in the above image?
It says annulus now!
Here is a way to get 9 regions.
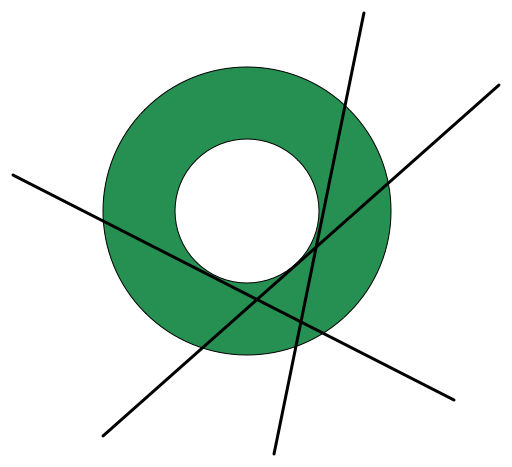
Note: It is not crucial for the lines to be tangential to the inner circle. All that is needed, is for the lines to touch/cut the inner circle, and also for the lines to intersect on the annulus.
I'm not immediately certain how to prove the general case. Thoughts?
It's actually pretty easy to come up with an idea to work in general case:
- Draw the small circle (the "hole").
- Choose 2 n points that are in a single semicircle. (One of the arcs formed is more than half of the perimeter.)
- Join each adjacent pair. (The two separated by the large arc aren't adjacent.)
- Extend the n segments infinitely.
- Draw the large circle so it encloses all the intersections and is concentric with the small circle.
- That's our annulus and lines.
The idea is that if we remove the hole, then our lines divide the large circle into the maximum number of regions (since each line intersects each other in the circle). However, our construction also makes sure that there is a region bounded by all lines simultaneously (each line forms one side of the region, and the large circle also forms one more). We draw the hole to break this region, cutting each side twice and thus breaking it into n regions (one for each vertex not on the large circle, and one that includes the arc unbroken).
(Note that it's actually not necessary for the large circle to also bound our region; we can also pick the 2 n points arbitrarily on the hole's perimeter, as long as after we pair them off, there's no parallel lines. It's just easier to explain; if an arc is more than half the perimeter, then it's guaranteed there are no parallel lines. Also, if the annulus is fixed, make one of the arcs in step 2 to be large enough to guarantee that the tangents at the two endpoints of the arc intersect inside the annulus, so that all intersections formed will also intersect inside the annulus..)
We have 1 + 2 n ( n + 1 ) regions from the circle, and we gain n − 1 new regions. This gives a total of 2 n ( n + 3 ) regions.
Log in to reply
Nice, I believe that works!
I don't understand Step 2. Could you draw an image?
This is superb. Mr calvin amazing.
I was going with the same approach in this problem, however, all of the three lines were intersecting at a single point, which means that the triangular piece wouldn't have been created.
The symmetrical solution is neater. See Armit Kazemi's solution. 7 May 2015.
6 + 0 = 6
6 + 1 = 7
6 + 2 = 8
6 + 3 = 9
Answer: 9
Could you please explain me in detail?
This is clearer than water!!!!!
I have no idea wjhat this all means.
My eyes are opened
best solution in the world right here. so good
Cut in a triangle shape (like in the problem picture), but every corner of the triangle must be inside the ring.
Make a triangle of 3 chords of which each corner shows a crossing chord ...now place this triangle on circle such as corners are placed on thick green area of the circle .. Now count the pieces...these are 9
Assuming it is a solid object in 3 dimensions, I was thinking of making a longitudinal cut first, and then two more like some of these chopsticks. Got to run right now, no time to think it out. Might be ten; two times five.
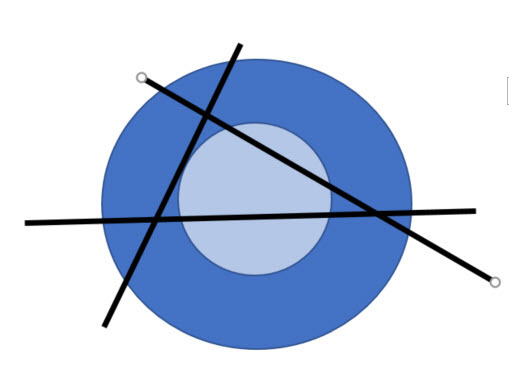
an annulus has a inner and outer circle. and we know that the maximum regions that 3 lines can make in a circle is 7. the region between three line's intersection is a triangle. so if the inner circle of annulus touch/cut each 2 sides of triangle - not the extensions of its sides-, there will be 3 more regions and -1 region (-1 is for the part of triangle which is in the inner circle) for the annulus. and by giving an example it can be proved.