Cutting an ellipsoid to specs
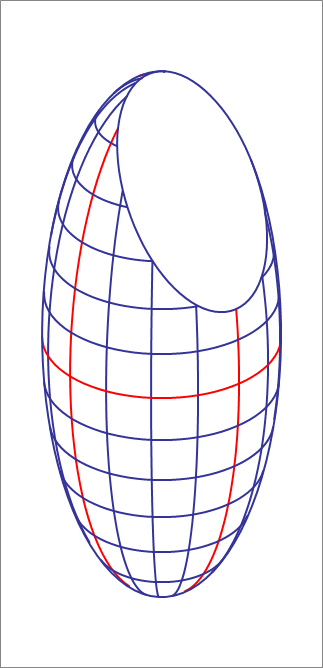
An ellipsoid of revolution is given by
1 0 2 x 2 + 1 0 2 y 2 + 2 5 2 z 2 = 1
Your task is to pass a cutting plane through the ellipsoid such that the intersection is an ellipse of semi-minor axis of length 5 and semi-major axis of length 10.
If the cutting plane has the unit normal vector n = ( sin θ cos ϕ , sin θ sin ϕ , cos θ ) , and it passes through the point ( 0 , 0 , z 0 ) . Find the angle θ , (expressed in degrees), and the z-intercept z 0 and submit their sum, using 3 significant figures.
Details and Assumptions:
- Since the ellipsoid is symmetrical about the z -axis, the angle ϕ can take any value.
- Since the ellipsoid is symmetrical about the x y plane, we will take θ ∈ [ 0 , 2 π ] , and z 0 ≥ 0 .
The answer is 104.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Method 1:
The equation of the ellipsoid can be written as:
r t Q r = 1
where Q = d i a g [ q 1 , q 1 , q 2 ] , and q 1 = 1 / 1 0 2 , q 2 = 1 / 2 5 2 . Assuming ϕ = 0 , the unit normal vector is n = ( sin θ , 0 , cos θ ) , and the z-intercept is r 0 = ( 0 , 0 , z 0 ) . The cutting plane is therefore spanned by any two linearly independent vectors that are orthogonal to the normal vector. We'll take these two vectors to be unit vectors and orthogonal to each other as well, the natural choice is:
v 1 = ( − cos θ , 0 , sin θ ) , and v 2 = ( 0 , 1 , 0 )
Now let V = [ v 1 , v 2 ] , then, points on the plane can be expressed as r = r 0 + V u , where u is the coordinate vector with respect to v 1 and v 2 .
To find the intersection between the plane and the ellipsoid we substitute this expression into the equation of the ellipsoid, this results in,
( r 0 + V u ) T Q ( r 0 + V u ) = 1
Expanding,
u T V T Q V u + 2 u T V T Q r 0 = 1 − r 0 T Q r 0
Define u 0 = − ( V T Q V ) − 1 V T Q r 0 , then
( u − u 0 ) T V T Q V ( u − u 0 ) = 1 − r 0 T Q r 0 + u 0 T V T Q V u 0 = C
Using the above definitions, it follows that
V T Q V = d i a g [ q 1 cos 2 θ + q 2 sin 2 θ , q 1 ]
V t Q r 0 = ( q 2 z 0 sin θ , 0 )
( V T Q V ) − 1 = d i a g [ 1 / ( q 1 cos 2 θ + q 2 sin 2 θ ) , 1 / q 1 ]
Further,
u 0 = − ( V T Q V ) − 1 V T Q r 0 = ( − q 2 z 0 sin θ / ( q 1 cos 2 θ + q 2 sin 2 θ ) , 0 )
and therefore,
u 0 t V T Q V u 0 = q 2 2 z 0 2 sin 2 θ / ( q 1 cos 2 θ + q 2 sin 2 θ )
and, also, r 0 T Q r 0 = q 2 z 0 2
Hence the constant C on the right hand side of the defining equation of the intersection ellipse above is given by,
C = 1 − z 0 2 q 2 + sin 2 θ q 2 2 z 0 2 / ( q 1 cos 2 θ + q 2 sin 2 θ )
Simplifying and re-arranging,
C = ( q 1 cos 2 θ + q 2 sin 2 θ − q 1 q 2 z 0 2 cos 2 θ ) / ( q 1 cos 2 θ + q 2 sin 2 θ )
Now the ratio of the minor to major axes lengths, when squared is exactly the ratio of the smaller eigenvalue to the larger eigenvalue of the matrix V T Q V .
Required ratio of semi-axes is 5 / 1 0 = r , then r 2 = ( q 1 cos 2 θ + sin 2 θ q 2 ) / q 1
Which is trivially easy to solve for θ , and it comes to, θ = 1 . 2 3 7 3 2 3 = 7 0 . 8 9 3 3 9 ∘
To determine z 0 , note that, a 2 1 = C q 1 = q 1 ( q 1 cos 2 θ + q 2 sin 2 θ ) / ( q 1 cos 2 θ + q 2 sin 2 θ − q 1 q 2 z 0 2 cos 2 θ )
This is also trivially solvable for z 0 , and the result is z 0 = 3 3 . 0 7 1 8 9 .
This makes the answer to the problem = 7 0 . 8 9 3 3 9 + 3 3 . 0 7 1 8 9 = 1 0 3 . 9 6 5 = 1 0 4 .
Method 2:
Squish the ellipsoid along the z-axis, by a factor of 2 . 5 1 , it becomes a sphere of radius 10.
The cutting plane in the original problem is transformed into a plane that cuts through the sphere. We can take the cutting plane normal to lie in the xz -plane. Let this plane have a unit normal vector of n = ( sin ψ , 0 , cos ψ ) and let it pass through the point p 0 = r 0 n , where r 0 < 1 0 . The intersection between the sphere and the plane is a circle of radius r = 1 0 0 − r 0 2 . Clearly, when we want to stretch the sphere back into the given ellipsoid, the diameter of the cut circle along the y-axis will remain unchanged. Hence and since the semi-minor axis length is 5, then r 0 = 7 5 .
The plane cutting through the sphere passes through the point ( 0 , 0 , r 0 / cos ψ ) . (This is easy to prove, and is left as an exercise to the reader). Further, the endpoints of the diameter of the intersection circle that lies in the xz plane are p 1 = r 0 ( sin ψ , 0 , cos ψ ) ± r ( cos ψ , 0 , − sin ψ ) .
Now if we stretch the sphere back into the given ellipsoid, this diameter becomes the major axis of the ellipse.
The semi-length is 10, so
1 0 2 = r 2 cos 2 ψ + 2 . 5 2 r 2 sin 2 ψ
Substituting r = 5 , and solving for ψ , we get ψ = 0 . 8 5 7 0 7 2 (radian)
Next we compute the corresponding θ . Starting from the equation of the plane cutting the sphere, which is,
( sin ψ , 0 , cos ψ ) ⋅ r = r 0
If we stretch back both the sphere and the plane, the image of a point, r = ( x , y , z ) , will be r ′ = ( x , y , 2 . 5 z ) a point on the stretched (desired) plane. Therefore, the equation governing r ′ is,
( sin ψ , 0 , cos ψ / 2 . 5 ) ⋅ r ′ = r 0
And this vector is a multiple of the desired unit normal vector = ( sin θ , 0 , cos θ )
Hence, tan ( θ ) = 2 . 5 tan ( ψ ) , from which, θ = 1 . 2 3 7 3 2 3 = 7 0 . 8 9 3 3 9 ∘
By the same token, z 0 = 2 . 5 7 5 / cos ψ = 3 3 . 0 7 1 8 9
This makes the answer = 7 0 . 8 9 3 3 9 + 3 3 . 0 7 1 8 9 = 1 0 3 . 9 6 5 = 1 0 4 when rounded to 3 significant digits
Let ϕ = 0 , so the plane that cuts the ellipse is parallel to the y -axis, and let it cut the ellipse at ( p , 0 , q ) and ( r , 0 , s ) . Since these points are on the ellipse, 1 0 2 p 2 + 1 0 2 0 2 + 2 5 2 q 2 = 1 or
2 5 p 2 + 4 q 2 = 2 5 0 0
and 1 0 2 r 2 + 1 0 2 0 2 + 2 5 2 s 2 = 1 or
2 5 r 2 + 4 s 2 = 2 5 0 0
Since the semi-major axis has a length of 1 0 , the distance between ( p , 0 , q ) and ( r , 0 , s ) is 2 0 , so by the distance formula, 2 0 = ( p − r ) 2 + ( 0 − 0 ) 2 + ( q − s ) 2 or
( p − r ) 2 + ( q − s ) 2 = 4 0 0
Finally, the minor axis would pass through the midpoint of ( p , 0 , q ) and ( r , 0 , s ) which is ( 2 p + r , 0 , 2 q + s ) . At that height, the ellipsoid has a cross-sectional circle of 1 0 2 x 2 + 1 0 2 y 2 + 2 5 2 ( q + s ) 2 = 1 , which has a radius of 1 0 0 − 2 5 ( s + q ) 2 . By Pythagorean Theorem, a semi-minor axis of 5 that goes through a point that is 2 p + r away from the center of this circle gives the equation ( 2 p + r ) 2 + 5 2 = 1 0 0 − 2 5 ( s + q ) 2 or
2 5 ( p + r ) 2 + 4 ( s + q ) 2 = 7 5 0 0
Solving these 4 equations gives positive solutions p = 7 5 2 1 , q = 1 4 1 2 5 7 , r = 7 1 5 2 1 , and s = 1 4 2 5 7 .
The plane horizontal to the y -axis through these points is 3 5 3 x + z = 1 4 1 7 5 7 , which has a z -intercept of z 0 = 1 4 1 7 5 7 ≈ 3 3 . 0 7 1 8 9 1 3 9 and a unit normal vector of ( 1 4 5 7 , 0 , 1 4 2 1 ) . Therefore, cos θ = 1 4 2 1 or θ ≈ 7 0 . 8 9 3 3 9 4 6 5 ° , and the sum of z 0 and θ is z 0 + θ ≈ 1 0 4 .