Cutting-edge Geometry
The entire surface of a cube with edge length , is painted. The cube is then cut into smaller cubes each with edge length . How many of the smaller cubes have paint on exactly one face?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
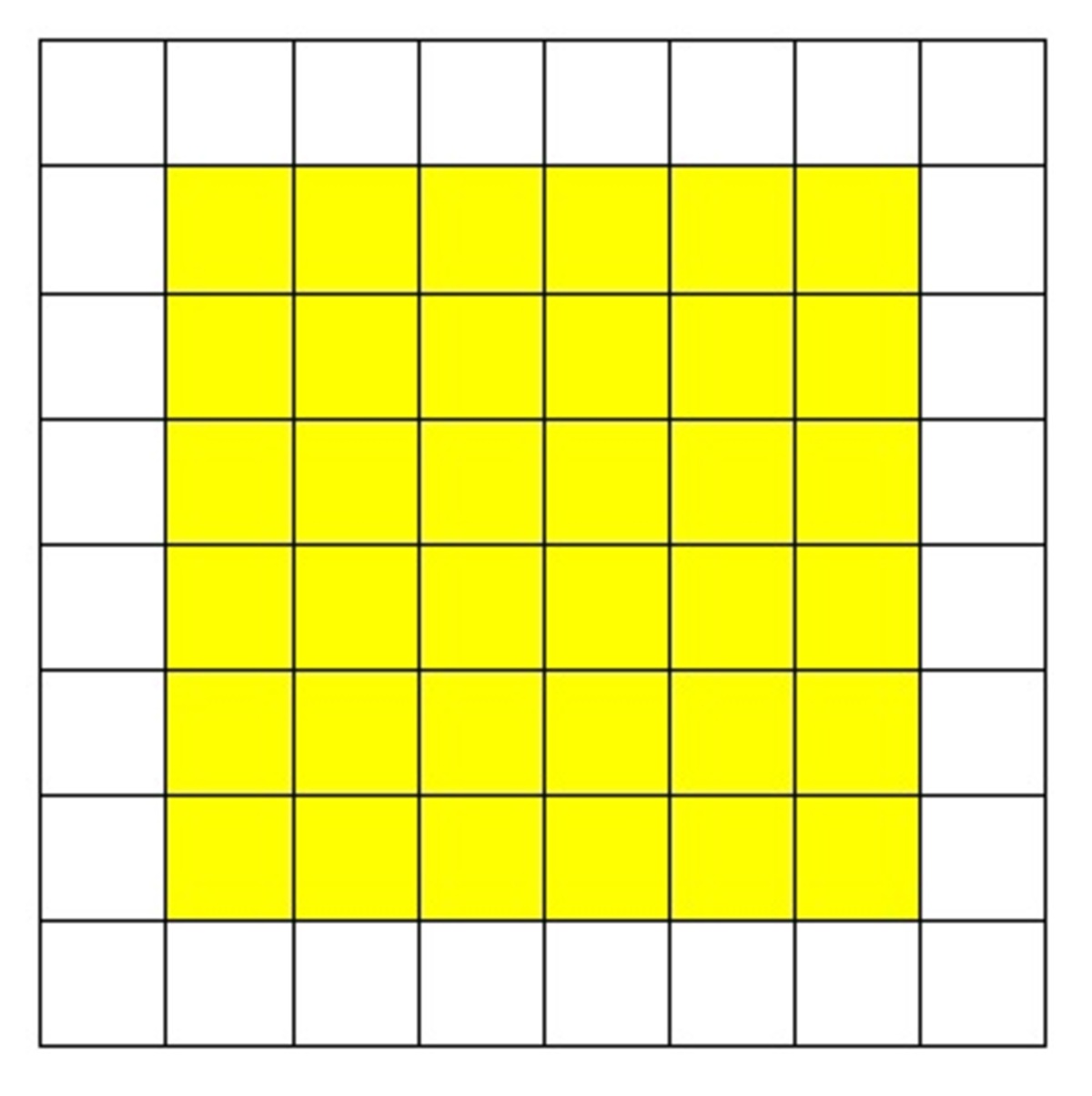Consider one face of the large cube, there are 36 small cubes that have paint on exactly one face. Since the large cube has six faces, then the number of small cubes that have paint on exactly one face is
6
(
3
6
)
=
2
1
6
.
