Cutting Paper

Geometry Level 3

Alice is desperately in need of a 6 cm × 2 cm 6\text{ cm}\times 2\text{ cm} rectangular sheet of paper for her school project. Unfortunately, she only has a 4 cm × 3 cm 4\text{ cm}\times 3\text{ cm} piece. So she decides to cut this paper into pieces such that rearranging them can give her a 6 cm × 2 cm 6\text{ cm}\times 2\text{ cm} rectangle.

What is the minimum number of cuts necessary to achieve this feat?

Note: A cut is a continuous division of a sheet of paper. An example is shown below:

1 2 3 4+

Ankit Agarwal by Ankit Agarwal , 22, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

David Vreken
May 22, 2018

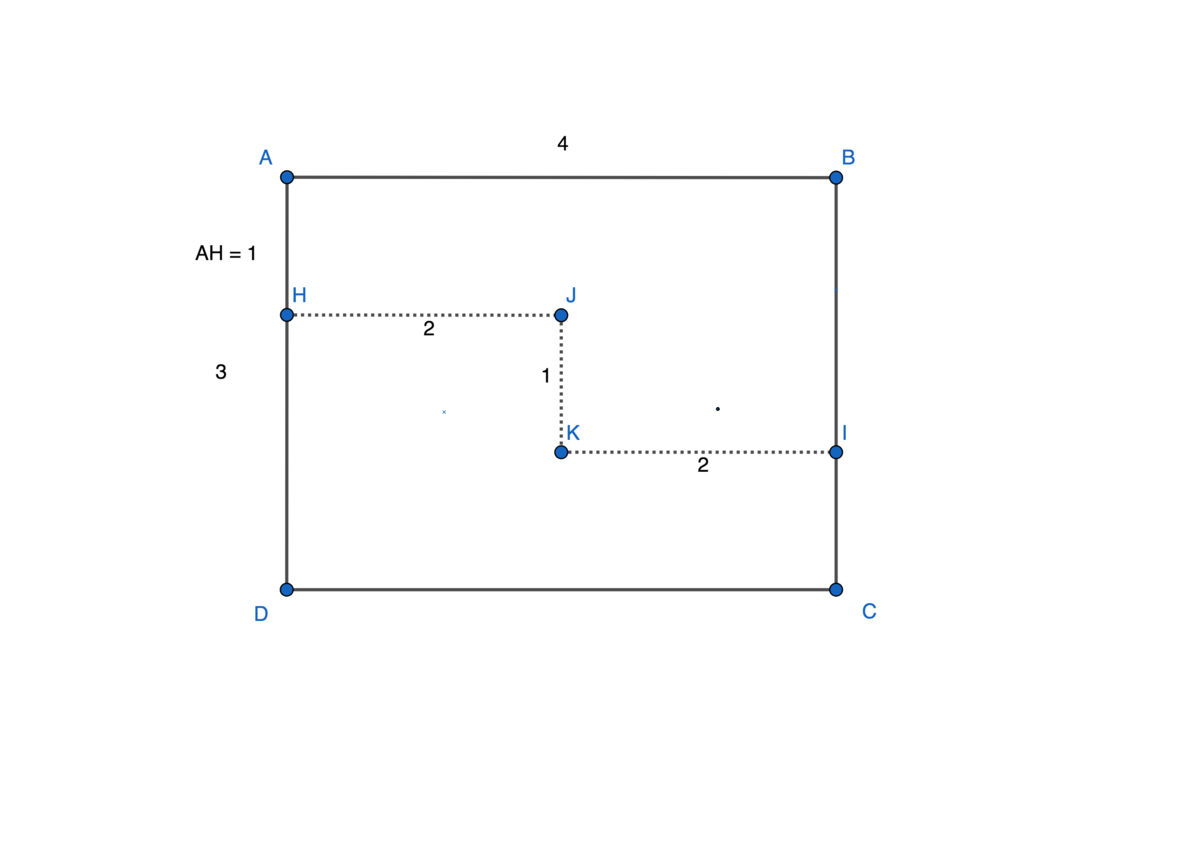
The 4 x 3 paper can be cut with 1 cut down its center to make two 2 x 3 rectangles. Then those two rectangles can be rotated 90° and attached to make one 6 x 2 paper.

3 Helpful 0 Interesting 0 Brilliant 0 Confused
Ankit Agarwal
May 21, 2018

The correct answer is 1 cut! In fact, she can accomplish this feat by following the cut shown below:

She can now separate the two pieces so that they can fit together in a 6 by 2 rectangle!

3 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...