Cutting The Paraboloid

The equation for the paraboloid is

$z = a x^2 + b y^2$

In matrix form, and by defining $r = [x, y, z]^T$ ,

$r^T A r + B^T r = 0$

where $A = \rm{diag} \{ a, b, 0 \}$ , and $B = [0, 0, -1]^T$

Points on the cutting plane, can be expressed as

$r = r_0 + Vu$

where $r_0$ , is any point on the plane, and $V = [ v_1, v_2 ]$ where $v_1$ , $v_2$ are any two unit vectors orthogonal to each other and to the normal to the plane.

Substituting this $r$ into the equation of the paraboloid,

$(r_0 + Vu)^T A (r_0 + Vu) + B^T (r_0 + Vu) = 0$

Expanding,

$r_0^T A r_0 + 2 r_0^T A V u + u^T V^T A V u + B^T r_0 + B^T V u = 0$

Collecting terms

$u^T V^T A V u + (2 r_0^T AV + B^T V ) u = - r_0^T A r_0 - B^T r_0$

Completing the square,

$(u - u0)^T V^T A V (u - u_0) = - r_0^T A r_0 - B^T r_0 + u_0^T V^T A V u_0$

where $u_0 = -1/2 (V^T A V)^{-1} (2 r_0^T A V + B^T V)^T$

Since $V^T A V$ is a symmetric matrix, there exists a 2x2 rotation matrix $R$ , and a 2x2 diagonal matrix $D$ , such that

$R^T V^T A V R = D$

setting $u = u_0 + R w$ , we get,

$w^T D w = c$

with $c = - r_0^T A r_0 - B^T r_0 + u_0^T V^T A V u_0$

Finally, dividing by c, we get

$w^T E w = 1$

where $E = D / c$

This is an equation of an ellipse with center $r_C = r_0 + V u_0$ .

If $E = \rm{diag} \{ e_{11}, e_{22} \}$ , then

the semi-major , and semi-minor axes lengths are

${ 1/ \sqrt{e_{11}}, 1/ \sqrt{e_{22}} }$

(Not necessarily in this order)

Performing the necessary calculations results in the following semi-major and semi-minor axes:

$M = 2.578468$

$m = 1.246847$

Hence the answer is $M + m = \boxed{3.825}$

I solved this problem in the "old-women" fashion, although I was very lucky in certain point. The first thing that I did was to get the $z$ from the first equation and substitute it in the second one. $\left. \begin{matrix} x+y+2z=2 \\ z={{x}^{2}}+\frac{1}{4}{{y}^{2}} \\ \end{matrix} \right\}\Rightarrow x+y+2{{x}^{2}}+\frac{1}{2}{{y}^{2}}=2$ This is a quadratic equation. At this point we can't actualy know this is an ellipse, it may be a hyperbola or a parabola as well, or even a pair of lines. There is a method called "reduction of quadratics to their canonical form", which transforms this quadratic into a more familiar form of a conic. It can be rewritten as: $2{{x}^{2}}+0\cdot 2xy+\frac{1}{2}{{y}^{2}}+\frac{1}{2}2x+\frac{1}{2}2y-2=0$ This one looks like this one: ${{a}_{11}}{{x}^{2}}+{{a}_{12}}2xy+{{a}_{22}}{{y}^{2}}+{{a}_{10}}2x+{{a}_{20}}2y-{{a}_{00}}=0$ Firstly we will apply the rotation to the quadratic. To determine the matrix of rotation the following matrix is formed: $A=\left( \begin{matrix} {{a}_{11}} & {{a}_{12}} \\ {{a}_{12}} & {{a}_{22}} \\ \end{matrix} \right)=\left( \begin{matrix} 2 & 0 \\ 0 & \frac{1}{2} \\ \end{matrix} \right)$ Then the eigenvalues and eigenvectors of $A$ are calculated. The unit vector of the eigenvectors will give the directions of the new coordinate system. For the eigenvalue ${{\lambda }_{1}}=2$ the eigenvector is ${{v}_{1}}=\left( \begin{matrix} 1 \\ 0 \\ \end{matrix} \right)$ . So its unit vector is ${{\vec{e}}_{1}}=\frac{{{{\vec{v}}}_{1}}}{\left\| {{{\vec{v}}}_{1}} \right\|}=1\vec{i}+0\vec{j}$ . Similarly the other unit vector is ${{\vec{e}}_{2}}=0\vec{i}+1\vec{j}$ . The matrix of rotation can be written now: $R=\left( \begin{matrix} {{e}_{1x}} & {{e}_{2x}} \\ {{e}_{1y}} & {{e}_{2y}} \\ \end{matrix} \right)=\left( \begin{matrix} 1 & 0 \\ 0 & 1 \\ \end{matrix} \right)$ Now the substitution of variables is made: $\left( \begin{matrix} x \\ y \\ \end{matrix} \right)=R\left( \begin{matrix} {{x}'} \\ {{y}'} \\ \end{matrix} \right)\Rightarrow \begin{matrix} x={x}' \\ y={y}' \\ \end{matrix}$ Now the translation part comes. Here we form perfect squares and try to bring the cuadratic in a known form. $2{{{x}'}^{2}}+\frac{1}{2}{{{y}'}^{2}}+\frac{1}{2}2{x}'+\frac{1}{2}2{y}'-2=0$ $2{{\left( {x}'+\frac{1}{4} \right)}^{2}}+\frac{1}{2}{{\left( {y}'+1 \right)}^{2}}-\frac{1}{8}-\frac{1}{2}-2=0$ Making the substitution $X={x}'+\frac{1}{4}$ and $Y={y}'+1$ the shifted conic becomes: $2{{X}^{2}}+\frac{1}{2}{{Y}^{2}}-\frac{1}{8}-\frac{1}{2}-2=0$ This is the same thing as: $\frac{{{X}^{2}}}{{{\left( \sqrt{\frac{21}{16}} \right)}^{2}}}+\frac{{{Y}^{2}}}{{{\left( \sqrt{\frac{21}{4}} \right)}^{2}}}=1$ So here is what we did until now:

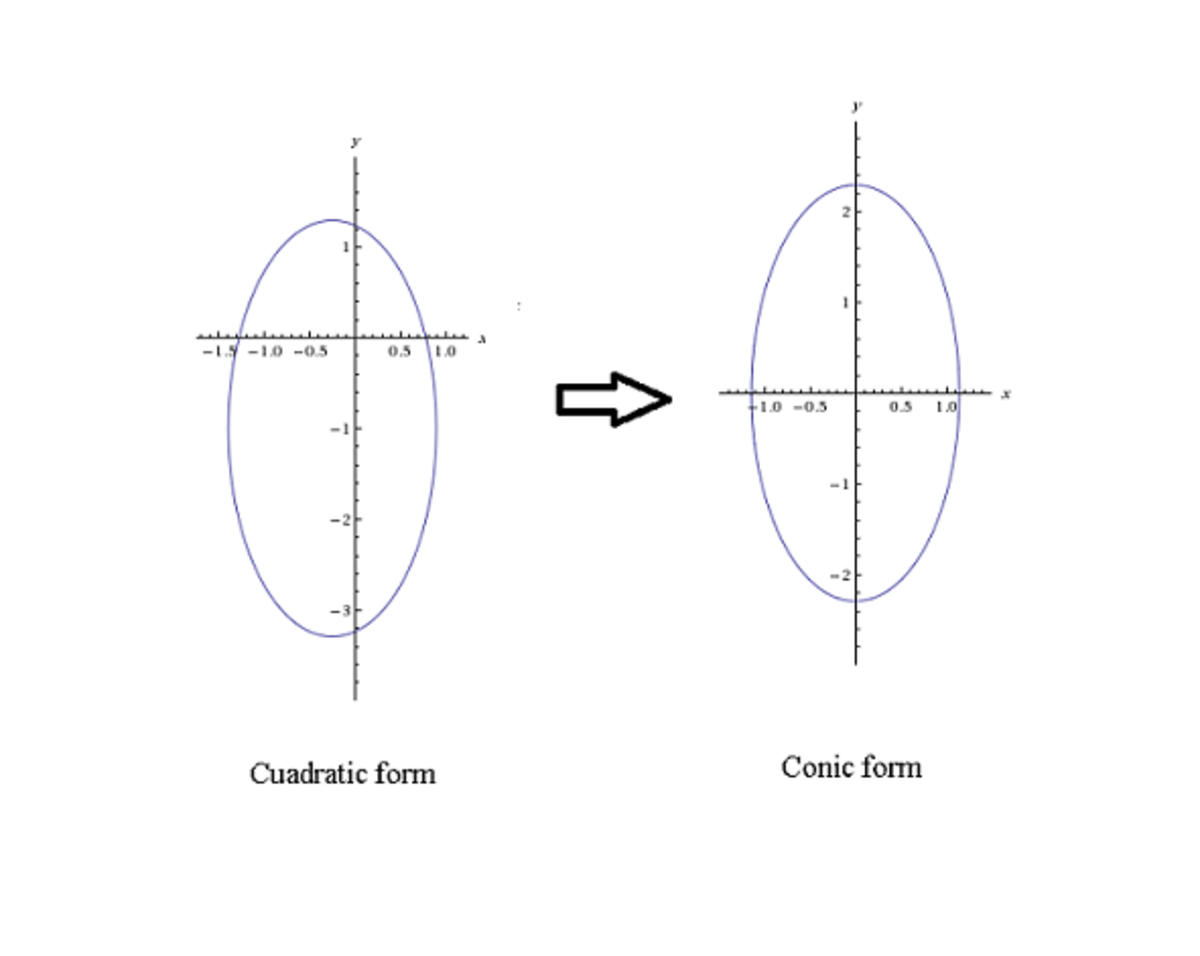
The thing is that this ellipse is the projection of the actual ellipse on the $xOy$ plane. And now comes the tricky part were I got lucky: the ellipse has its minor and major axes parallel to the coordinate axes. So by taking the derivative in respect to $x$ of the plane function we get $-0.5$ . This means that the slope in $x$ direction is $-0.5$ . The same is in $y$ direction. Now we can think at a right angle triangle with the length of base given (the minor and major axes of the projection conic) and with the ratio of the cathetus also given (the slopes in x and y direction). Basicaly we project this ellipse's major and minor axes back on the original inclined plane. The final answer is: $S=\sqrt{\frac{21}{16}}\sqrt{{{1}^{2}}+{{0.5}^{2}}}+\sqrt{\frac{21}{4}}\sqrt{{{1}^{2}}+{{0.5}^{2}}}=3.84267$

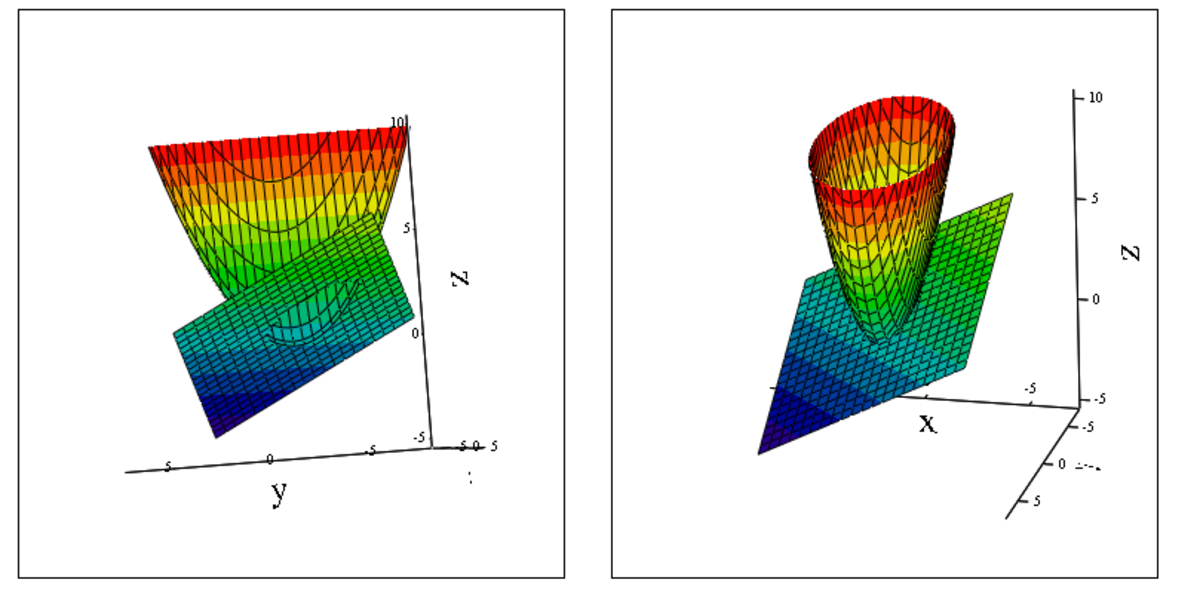
If the projected ellipse was rotated i would have tried to take some directional derivatives to calculate the back-projected lengths of major and minor axes. Fortunately I didn't have to do it.