Cutting up the Hexagon

The small red and blue triangles are congruent because they are both right triangles, share a hypotenuse, and their smallest angle is $30^\circ$ .

The smallest angle of the blue triangle is half of the internal angle of an equilateral triangle, $\dfrac{60^\circ}{2}=30^\circ$ .

The smallest angle of the red triangle can be calculated from the internal angle of a hexagon, $120^\circ$ , minus internal angle of an equilateral triangle, $60^\circ$ , (this will give us the total of all both red angles at the vertex) divided by $2$ .

$\dfrac{120^\circ-60^\circ}{2}=30^\circ$

The blue area is made up of 12 little blue triangles, the red are is made up of 12 little red ones, so the two areas are the same.

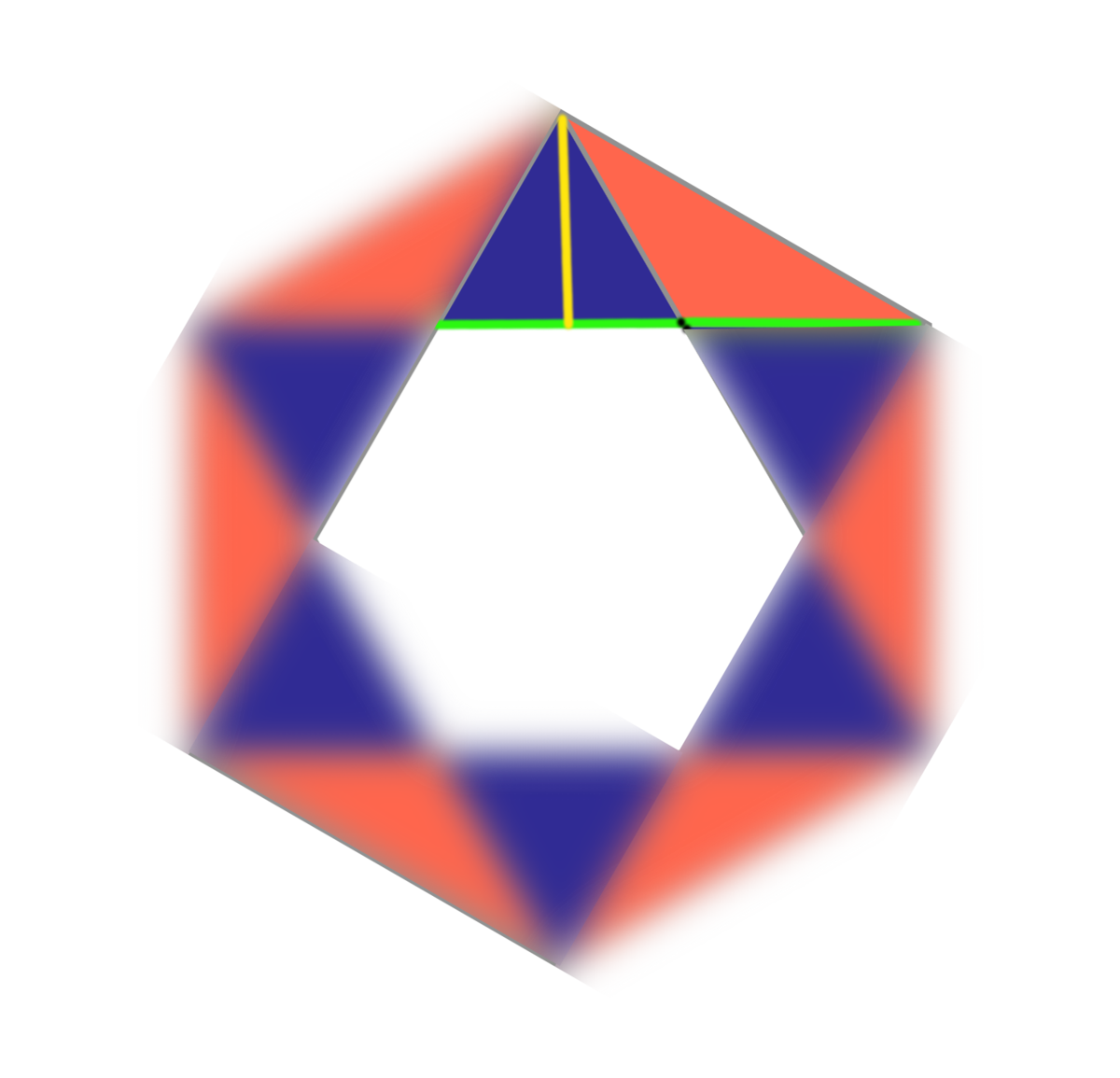
The two green segments are equal, and the yellow segment is their common height

If you create a rectangle out of two blue and two red triangles, then the area of one red triangle would be $\frac{1}{2}$ X Length X $\frac{1}{2}$ X Width, or $\frac{1}{4}$ X Length X Width. This is the same for the blue triangles as the base is the width and theheight is half of the length. Therefore the area of the blue triangle is also $\frac{1}{4}$ X Length X Width. As there are 6 blue and 6 red triangles, the overall areas are the same.

Consider a blue and an adjacent red triangle. They form one triangle. So the blue and red trinagle have the same height. They also have the same base (as is evident from the other blue triangle). So, they have the same area. There is an equal number of red and blue triangles. Hence, the red and blue areas are equal.

Let $b$ represent the length of the longest side of a Orange Triangle, so the base of a Orange Triangle, $b_{O}$ , is equal to $b$ . The height of a Blue Triangle, $h_{B}$ , is needed twice to make up the length of $b$ , so $h_{B} = \frac{b}{2}$ . The height of the Orange Triangles, $h_{O}$ , is similarly needed twice to make up the length of the base of the Blue Triangles, $b_{B}$ .

Since the area of a triangle is equal to $\frac{1}{2}bh$ , the area of the Blue Triangles is equal to $\frac{1}{2}*b_{B}*h_{B} = \frac{1}{2}*b_{B}*(\frac{b}{2}) = \frac{b_{B}b}{4}$

and the area of the Orange Triangles is equal to $\frac{1}{2}*b_{O}*h_{O} = (\frac{b}{2})*(\frac{b_{B}}{2}) = \frac{b_{B}b}{4}$

Thus, $A_{B} = A_{O}$ and so $6*A_{B} = 6*A_{O}$ , meaning the colored areas area equal.

A median in a triangle divides it into two triangles with equal areas.

A blue triangle and an orange triangle have the same height and their bases are of equal lengths, so they have equal areas, and thus 6 blue triangles have the same area as 6 orange triangles.

Another solution.

Everytime A=B

No any number in the question. You can guess the this rule.

Let's call $a$ the side of the purple triangle. Now area of each purple triangle is $(1/2) a^2 \sin(60^o)$ .

Also the area of each orange triangle is $(1/2)a^2 \sin(120^o)$ , which is the same as the purple triangle. And there are 6 each of both orange and purple triangles.

So both equal.

Look, there r identical 6 red colored triangles and another identical 6 purple colored triangles. So our destination will be to measure area of each triangle and compare between them. As the base of each red and purple colored triangle are same and also their height. that means area of these triangles are same. so we can finally say are of red =purple.