Cyclic Bisecting
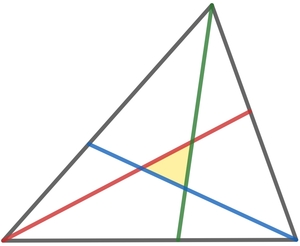
In the given figure, the area of the black triangle is 1.
Also, the green line bisects the blue line, the blue line bisects the red line and the red line bisects the green line.
Find the area of the yellow region.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
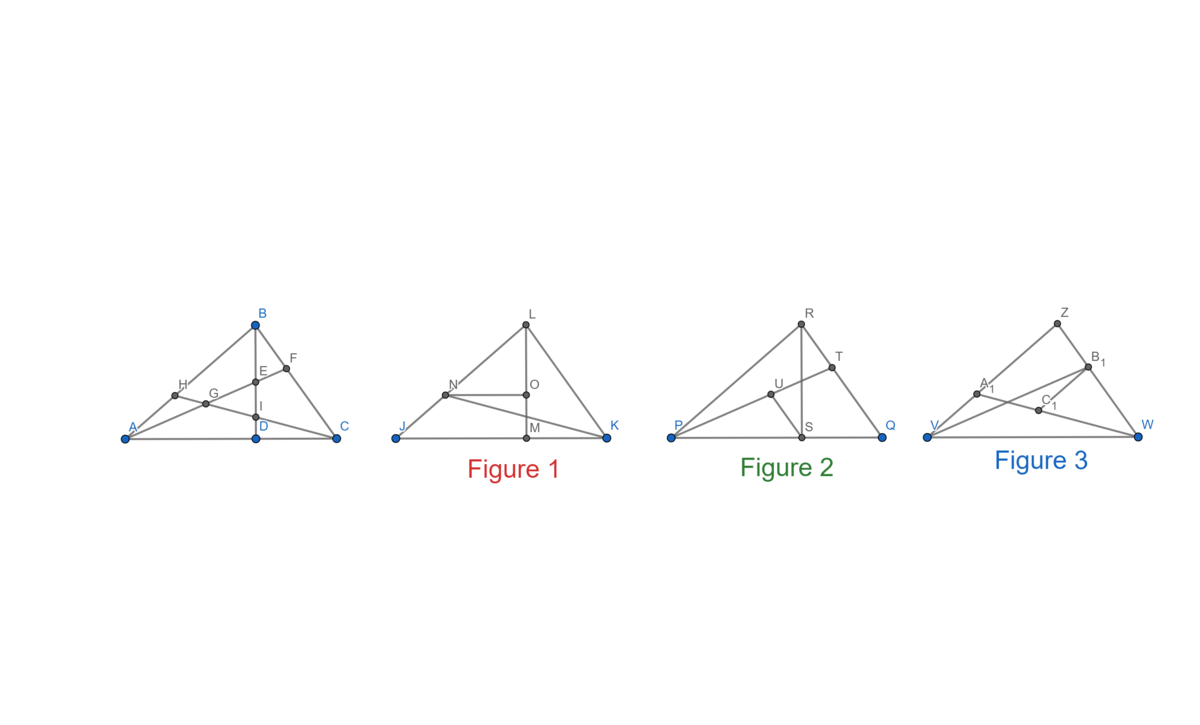
First consider an equilateral triangle with the same conditions, labelled as follows:
By rotational symmetry, A 1 = A 2 = A 3 , B 1 = B 2 = B 3 , and C 1 = C 2 = C 3 .
Since P X = X U , A 1 + B 1 = A 2 + C 1 and A 3 + B 3 + C 3 = D + B 2 + C 2 . Using the above equations, we can deduce that B 1 = C 1 and A 3 = D (so B 1 = B 2 = B 3 = C 1 = C 2 = C 3 and A 1 = A 2 = A 3 = D ).
Examining triangles with a side ratio of X Y P X , we have C 1 A 1 + B 1 = D C 3 , and using the above equalities this becomes B 1 D + B 1 = D B 1 , which simplifies to B 1 = 2 1 + 5 D (the golden ratio!)
Since the area of the triangle is 1 , we have A 1 + A 2 + A 3 + B 1 + B 2 + B 3 + C 1 + C 2 + C 3 = 1 , or 4 D + 6 B 1 = 1 .
Solving B 1 = 2 1 + 5 D and 4 D + 6 B 1 = 1 gives D = 4 7 − 3 5 .
Since any triangle with the same area can be transformed to this equilateral triangle by shear mapping , which also preserves areas and length ratios, this value of D is true for any triangle with an area of 1 .