Cyclic equations
For an integer n > 2 , we have real numbers a 1 , a 2 , a 3 , a 4 , . . . , a n such that a 2 + a 3 + a 4 + ⋯ + a n a 1 + a 3 + a 4 + ⋯ + a n a 1 + a 2 + a 3 + ⋯ + a n − 1 = a 1 = a 2 ⋮ = a n .
What is the value of a 1 + a 2 + a 3 + ⋯ + a n ?
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
∑ l h s = ∑ r h s ( n − 1 ) ∑ a i = ∑ a i ( n − 2 ) ∑ a i = 0
Let us consider the equations for
a
1
,
a
2
&
a
3
.
a
2
+
a
3
+
a
4
+
…
=
a
1
→
E
q
.
1
a
1
+
a
3
+
a
4
+
…
=
a
2
→
E
q
.
2
a
1
+
a
2
+
a
4
+
…
=
a
3
→
E
q
.
3
E
q
.
1
&
E
q
.
2
may be rearranged as:
−
a
1
+
a
2
+
a
3
+
a
4
+
…
=
0
→
E
q
.
A
&,
a
1
−
a
2
+
a
3
+
a
4
+
…
=
0
→
E
q
.
B
Subtracting
E
q
.
A
f
r
o
m
E
q
.
B
, we get,
2
a
1
−
2
a
2
=
0
⇒
a
1
−
a
2
=
0
a
1
=
a
2
Now, rearranging
E
q
.
3
,
a
1
+
a
2
−
a
3
+
a
4
+
…
=
0
→
E
q
.
C
Subtracting
E
q
.
A
from
E
q
.
C
, we get,
2
a
1
−
2
a
3
=
0
⇒
a
1
−
a
3
=
0
a
1
=
a
3
On repeating the process with other variables, we can see that,
a
1
=
a
2
=
a
3
=
a
4
=
…
=
a
n
→
E
q
.
4
But, we also know that the value of any one variable is equal to the sum of all the other variables.
Combining the above condition with
E
q
.
4
leaves us with only one possible value that can be assigned to the variables while satisfying both the conditions at hand, i.e
0
.
So,
a
1
=
a
2
=
a
3
=
a
4
=
…
=
a
n
=
0
Hence,
a
1
+
a
2
+
a
3
+
a
4
+
…
+
a
n
=
[
0
+
0
+
0
+
…
n
t
i
m
e
s
)
]
=
0
Log in to reply
nice approach and thinking....
a 1 + a 2 could be anything you want when n = 2 , so it should be added to the problem that n ≥ 3 , n ∈ N .
Log in to reply
oh yes...i was kinda rush =.=
Yeah, I got it wrong the first time because of that.
Correct. That's what I too observed.
its a silly problem, one just has to restate the question in one's words....does it matter that a negative coefficient appears in a given set of equations from n=1 to n=n where n is index that all equal to 0. in other words Matrix with diagonal of -1, has at least one solution, ... the answer is yes, if you can get that matrix to look like idetety matrix, then there is at least one solution....to adition of all a's 0
All that is fine and dandy, except that if you follow the logic of the problem [i.e. a(1) + a(2) + ... + a(n) - a(i) = a(i)], and then add each of the right hand side equations while substituting each for its longer form, you end up with (n-1) = [a(1) + a(2) + ... + a(n)]/[a(1) + a(2) + ... + a(n)] = 1; therefore, n = 2 for all a(i) regardless of what the equations "look" like. Following this, any value for a(i) works, as long as that the problem is limited to only two terms--a(1) = a(2).
Any assumptions beyond this are actually not valid. While 0 is a possible soultion, so are all real numbers.
T= a sub1 + a sub2 +... + a sub n a sub n = T - a sub n therefore 2a sub n = T a sub n = 1/2 T T = 1/2T + 1/2T... T = 1/2T(n) Anything multiplied by zero is always zero is the multiplicative property of zero. T = T(1/2n) so basically T = 0
from the given two lines in the question if we subtract those two line we get a1=a2 similarly a1=a3 and goes on so a1,a2,a3,.......,an are same number now only zero can be expressed as some of infinite zeros so zero is the answer
as we can see that each no. appears (n-1) times adding equations we get (n-1)(a {1}+a {2}....a {n})=(a {1}+a {2}....a {n}) therefore (a {1}+a {2}....a_{n})=x then (n-1)x=x (n-1)x-x=0 x(n-1-1)=0 x=0 or n=2 but n>2 so x=0. Q.E.D.
By subtraction, a1 is equal to a2. There is no answer to the problem because the true answer is 2x a1
No, for a1=a2, a1+a3+...+an=a2=a1 meaning that a3+a4+...an=0, and by manipulating the last equation we get 2a1+0-Ana=an, so a1=an, and we can also get that 2a2=0 by adding up 2 equations, and thus a1=a2=0, and ergo the answer is 0
i just thought that each number should be equal with other number and equal with the product too so the only correct answer is 0 :P
If we write these equations in the matrix form, AX=b where, b is a column matrix of order nX1 filled with 0's, A is a matrix of order nXn with diagonal filled with -1's and the rest of the matrix filled with 1's and x is a column vector with entries a1 to an, then the determinant of matrix A has to be zero in order to have atleast one non-zero among a1 to an. Here, the determinant of matrix A is zero. So, the values of all the variables a1 to an is 0.
Log in to reply
For n = 3 , the columns of A are linearly independent. Hence Ax=0 has only the trivial solution, so the sum of the entries is zero.
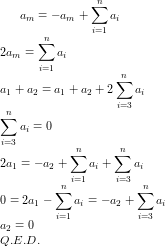
The only way any version of something added to itself could equal itself is if the original value was zero.