Cyclic Quadrilateral
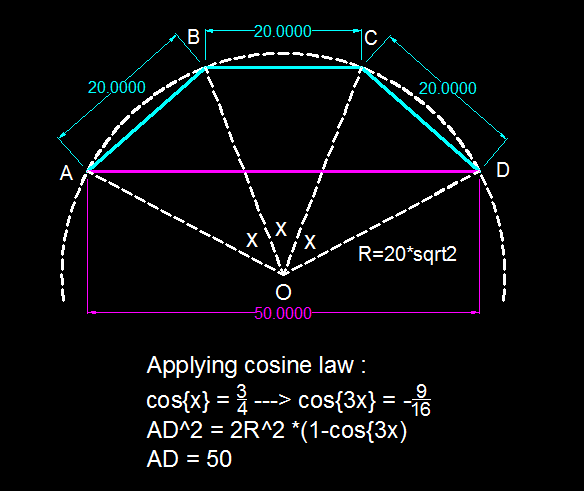
A B C D is a cyclic quadrilateral inscribed in a circle with radius 2 0 2 . Given that A B = B C = C D = 2 0 , what is the length of A D ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Non-trig solution:
Note: There are at least seven ways to solve this. This is just the way I solved it.
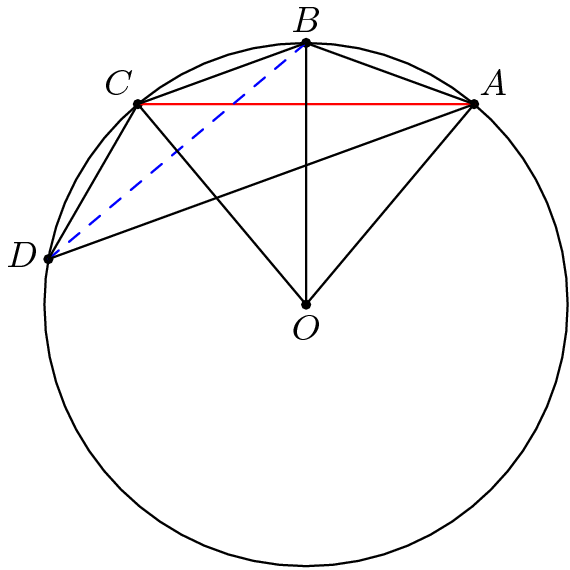
Let O be the center of the circle, and x be the shorter altitude of △ O B C . The length of x is 2 1 the length of A C .
By the Pythagorean Theorem, the longer altitude of △ O B C is 1 0 7 . We can therefore compute the area of △ O B C to be 1 0 0 7 .
Using the formula for the area of a triangle,
2 1 ⋅ 2 0 2 ⋅ x = 1 0 0 7
Solving for x yields x = 5 1 4 . Therefore, the length of A C is 1 0 1 4 .
By Ptolemy's Theorem ,
1 0 1 4 ⋅ 1 0 1 4 = 2 0 ⋅ 2 0 + 2 0 ⋅ A D
1 4 0 0 = 4 0 0 + 2 0 ⋅ A D
A D = 5 0