Cyclic quadrilateral and the diameter
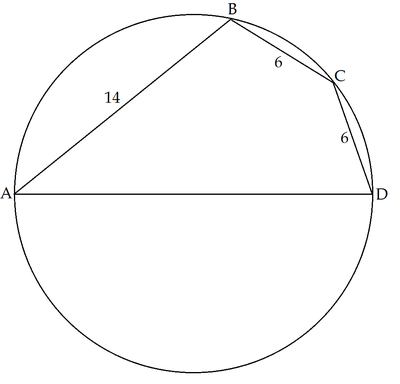
Quadrilateral A B C D is inscribed in a circle. It has side lengths A B = 1 4 , B C = 6 , C D = 6 , and A D being the diameter of the circle. What is the radius of the circle.
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let the center of the circle be ' O '. Join O B , O C . Let ∠ O D C = ∠ O C D = ∠ O C B = ∠ O B C = α . Then ∠ O A B = ∠ O B A = π − 2 α (Sum of opposite angles of a cyclic quadrilateral is π ). Now, using sine rule we can write sin α r = sin 2 α 6 ⟹ r = cos α 3 , where r is the radius of the circle. And sin ( π − 2 α ) r = sin ( 4 α − π ) 1 4 ⟹ r = − cos 2 α 7 = − 2 cos 2 α − 1 7 . Therefore cos α 3 = 1 − 2 cos 2 α 7 ⟹ 6 cos 2 α + 7 cos α − 3 = 0 ⟹ cos α = 3 1 . Hence r = 3 1 3 = 9 .
Let the diameter of the circle be A D = d . Since A D is a diameter, ∠ A B D = ∠ A C D = 9 0 ∘ . Also since A B C D is a cyclic quadrilateral , we can apply Ptolemy's theorem .
A C × B D d 2 − 6 2 × d 2 − 1 4 2 d 4 − 2 3 2 d 2 + 7 0 5 6 d 3 − 2 6 8 d − 1 0 0 8 ( d − 1 8 ) ( d + 4 ) ( d + 1 4 ) ⟹ d = B C × A D + A B × C D = 6 d + 1 4 × 6 = 3 6 d 2 + 1 0 0 8 d + 7 0 5 6 = 0 = 0 = 1 8 Squaring both sides Since d > 0
Therefore the radius of the circle is 2 d = 2 1 8 = 9 .