Cycloidish
A rectangle rolls on a flat surface, and the path of one of its vertices is traced as the rectangle rolls.
If the shorter side of the rectangle is 1 and the area under the traced path is 3 π , what is the length of the longer side of the rectangle?
The answer is 1.940300568.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Ughh I though it would br a simpler method than this
Log in to reply
For one, I wanted to area to be the same as the cycloid. I just realized the devs took out that part. For another, I thought the formula had a nice form, so I wanted solvers to need to derive it.
Math is never truly simple.
I'd say this solution is rather quite simple.
is there a more elegant way?
Log in to reply
define "elegant"
Do you like this way? 👆👆👆👆
Other way
A=3π
a=1
b=√((c^2)-1)
A1=πa^2/4=π/4
A2+A4=ab=b
A3=πc^2/4
A5=πb^2/4
3π=A1+A2+A3+A4+A5
3π=(π/4)((1+b+c)^2)+b
c^2=(3π-(π/4)-(πb^2/4)-b)/(π/4)
b=√((c^2)-1)
b=√{[[3π-(π/4)-(πb^2/4)-b]/(π/4)]-1}
b≈1.94
I truly enjoyed this problem. Thank you for posting it. It's a great way to show the importance of simplifying as much as possible before approximating pi.
The idea that the purple section is a quarter circle is assumed. To prove it you could show that the diagonals are negative reciprocols or that the combined angles are complementary and therefore 90 deg.
Log in to reply
No, it is 9 0 ∘ because you rotate it by 9 0 ∘ . What is it to prove?
I did it this way, and I feel this problem should have been placed under "Advanced" instead.
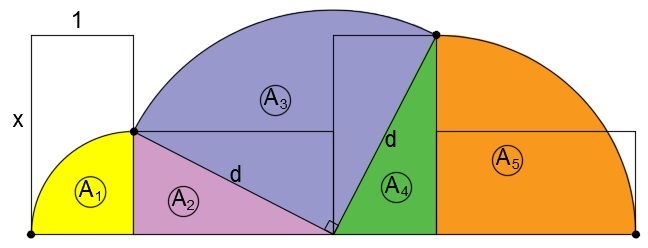 Consider my diagram.
Consider my diagram.
d = 1 + x 2
A 1 = 4 1 π = 4 π
A 2 = 2 1 ( 1 ) ( x ) = 2 x
A 3 = 4 1 π ( 1 + x 2 ) 2 = 4 π ( 1 + x 2 ) = 4 π + 4 π x 2
A 4 = A 2 = 2 x
A 5 = 4 1 π x 2 = 4 π x 2
The total area is 3 π . So,
3 π = A 1 + A 2 + A 3 + A 4 + A 5
3 π = 4 π + 2 x + 4 π + 4 π x 2 + 2 x + 4 π x 2 = 4 2 π x 2 + 4 2 π + 2 2 x
6 π = π x 2 + π + 2 x
π x 2 + 2 x − 5 π = 0
It ends up on a quadratic equation. By using the quadratic formula, we get
x ≈ 1 . 9 4 0 3 0 0 5 6 8
if the figure was sliding with 1unit dist/unit time , how do we calculate now since the segments now are not circles
Very nasty numbers, probably because I'm a high school student. Basically if you can see the 3 important length and know your quadratic formula, you are good to go!
Let the long side be L, why is solving (1/4) Pi+int(sqrt(L^2-x^2+1), x = -L .. 1)+(1/4) L^2 Pi = 3 Pi wrong?
Log in to reply
What is x in your comment?
Use latex. Very unclear
Assuming L is the long side and x is the shorter side (which was given, by the way); your problem is in your Pythagorean Theorem usage. The two terms should be added as L is not the radius of the central radius. The rightmost radius is L, however no Pythagorean Theorem is necessary to obtain that result.
..haha he said he’s high!
That is amazing! I made mine in Desmos too, but without animation and a fixed length.
Nice graph.
The blue and pink together make a rectangle of area a b
The green and orange are quarter-circles of radius a and b so their areas are 4 1 π a 2 and 4 1 π b 2
The large purple quarter circle has radius a 2 + b 2 so its area is 4 1 π ( a 2 + b 2 )
Therefore the area formula for the cycloidish shape is A = a b + 4 1 π a 2 + 4 1 π b 2 + 4 1 π ( a 2 + b 2 )
Which simplifies to A = 2 π ( a 2 + b 2 ) + a b
Letting a = 1 and b = x , an equation to find side length that gives area 3 π is
2 π ( 1 + x 2 ) + x = 3 π
This is a quadratic solution whose positive solution is
x = π − 1 + 1 + 5 π 2 ≈ 1 . 9 4 0 3 0 0 5 6 8