Cylinder says "Don't roll. Just hang on."
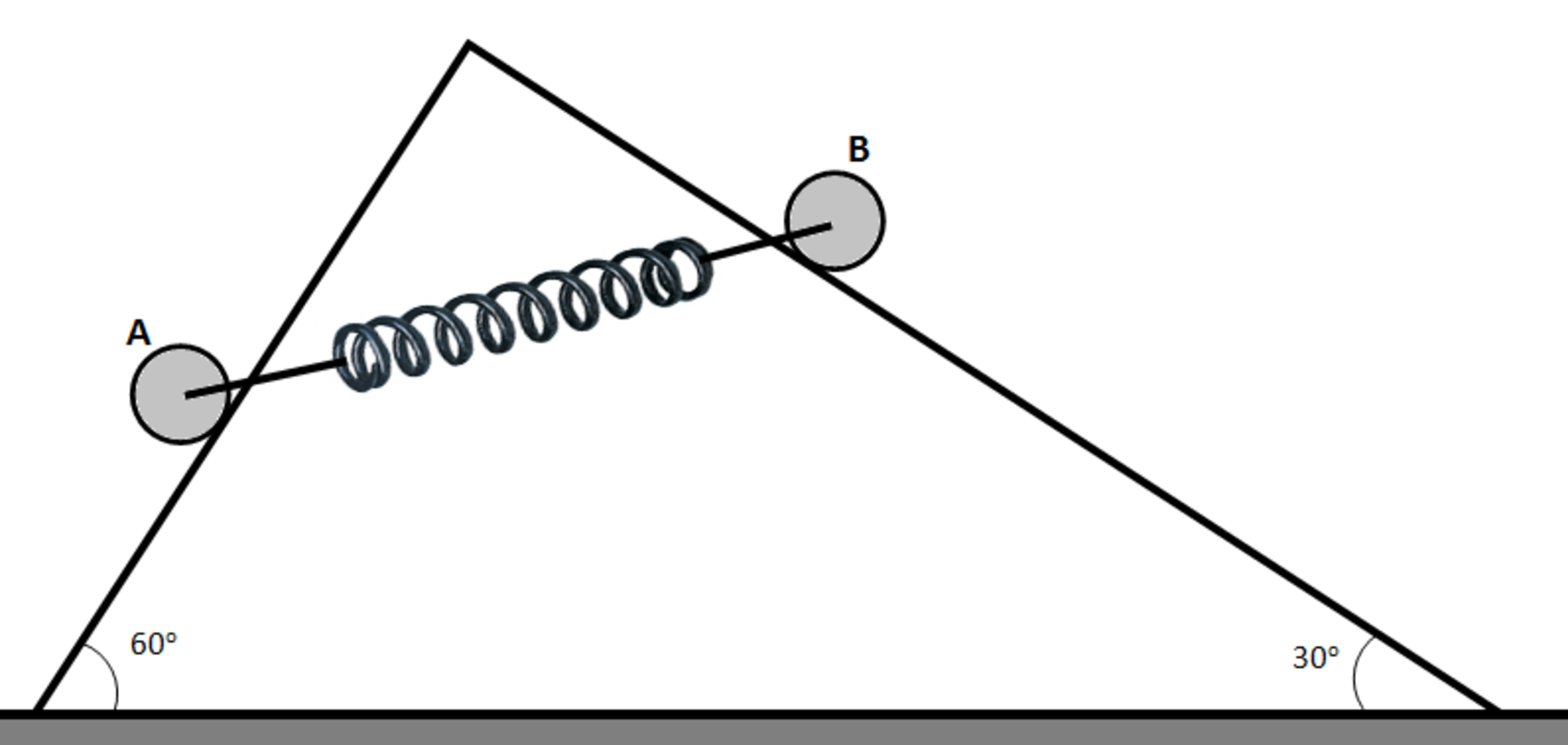
Two uniform solid cylinders A and B each of mass are connected by a light spring of force constant at their axles and are placed on a fixed wedge as shown in the figure. The coefficient of friction between the wedge and the cylinders is .
If is the elongation in the spring at equilibrium then find .
Take .
The answer is 8.487.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
In equilibrium, there will be no torque about the center of mass, and so the frictional forces must be zero.
Say the spring makes an angle θ with the horizontal. Then considering the net force along the slope for mass A gives:
sin ( π / 3 ) m g = k x cos ( π / 3 − θ )
and considering the net force along the slope for mass B gives:
sin ( π / 6 ) m g = k x sin ( π / 3 − θ )
Square each side of the equations, add the left sides and right sides, then take the square root, and you will see m g = k x so that 1 0 0 x = 1 0 0 k m g = 4 . 9 3