Cylinder's back against the wall
Rotating cylinders are not just physical abstractions: for example, they can turn a flow of the air, thus creating lift as the airplane wings. Historically people have even used rotating cylinders to power ships (although with little efficiency). NASA wrote more about this here .
We will now examine how much time we need to stop a ship-engine-like cylinder. Suppose you take a rotating cylinder and let it roll to the right until it reaches a vertical wall. It then spins against the two walls as shown in the picture, slowly slowing down. How much time will it take in s for the cylinder to stop?
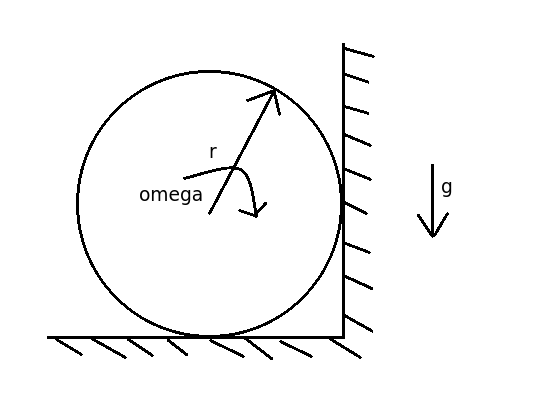
Details and assumptions
- The initial speed of the cylinder's surface when it touches the vertical wall is 3 0 m/s .
- Its length is l = 1 0 m , its radius is r = 0 . 5 m and it's made out of wood of density ρ = 8 0 0 kg/m 3 .
- The coefficient of friction between the cylinder and the walls is μ = 0 . 3 .
- The acceleration of gravity is − 9 . 8 m/s 2 .
- There are at least two ways to approach this problem.
The answer is 4.278.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Its 4.277 :P Haha!
There are five forces on the cylinder that we must consider:
- The downward force due to gravity.
- The upward normal force from the floor.
- The rightward force due to friction from the floor (this is what is normally responsible for the cylinder rolling to the right).
- The leftward normal force from the wall.
- The upward force due to friction from the wall.
Since the cylinder remains in the same location after hitting the wall, its net acceleration is 0 so these five forces must sum to 0. Label these forces F 1 , F 2 , F 3 , F 4 , F 5 , where F i corresponds to the above list item i . Now, F 1 = m g , and from the definition of the coefficient of friction we know that F 3 = μ F 2 and F 5 = μ F 4 . Since the only two horizontal forces must balance, we must have that F 4 and F 3 must be equal in magnitude, so we can write F 4 = μ F 2 and F 5 = μ 2 F 2 . Finally, the three vertical forces must balance, so we have that
F 2 + F 5 = ( 1 + μ 2 ) F 2 = m g
and therefore F 2 = 1 + μ 2 m g .
Now that we know the magnitudes of all the forces, let's consider the different torques. Forces F 3 and F 5 both exert a counterclockwise torque that will slow the rotation of the cylinder. This total torque has magnitude
τ = 1 + μ 2 μ + μ 2 m g r
Since τ = I α , and since the moment of inertia for a cylinder is given by
I = 2 m r 2
we have that the angular deceleration has magnitude
α = I τ = 1 + μ 2 μ + μ 2 ⋅ r 2 g
Finally, since ω = r v , we have that
t = α ω = μ + μ 2 1 + μ 2 ⋅ 2 g v ≈ 4 . 2 7 8
Woah your solution is well explained. I can't do it any better.
It's really a descriptive one. I must admit.
Let the friction force acting on the cylinder by the vertical wall and by the (horizontal) ground be F v and F h respectively. Also, let the normal force acting on the cylinder by the vertical wall and by the ground be N v and N h respectively. Then we have F v = μ N v and F h = μ N h . Note that there is also a downward force m g (due to gravity) acting on the cylinder of mass m . Resolving horizontal forces, we have F h = N v . Resolving vertical forces, we have F v + N h = m g . We can solve these four equations** to get F h = 1 + μ 2 m g μ and F v = 1 + μ 2 m g μ 2 . So the total force acting on the cylinder is F = F h + F v = 1 + μ 2 m g μ ( 1 + μ ) .
Now, we consider the change in angular momentum of the cylinder as it comes to a stop. This is given by d t d L = − r F , so we get L = − r F t + C for some constant C . When t = 0 , we know that C = L = I ω , where I = 2 m r 2 is the moment of inertia of the cylinder about the axis of rotation. Since ω = r v , then L = − r F t + r I v . When the cylinder comes to a stop, we have L = 0 , so t = r 2 F I v . This gives us t = 2 g μ ( 1 + μ ) v ( 1 + μ 2 ) . Substituting v = 3 0 , μ = 0 . 3 , g = 9 . 8 , we get t = 4 . 2 7 8 seconds.
**How do you solve those four equations? From the last equation, we have μ F v + μ N h = μ m g . Using the first two equations, this becomes μ 2 N v + F h = μ m g . Using the third equation, this becomes μ 2 F h + F h = μ m g , so we can solve for F h . Then we can solve for F v using F v = μ N v = μ F h .
We solve this problem by looking at the forces associated to the spinning cylinder. We can write the net torque acting on the cylinder as τ = r × F . The two forces are simply friction, and we can equate this to the moment of inertia times the angular acceleration, r ( μ F N 1 + μ F N 2 ) = I α , where F N 1 is the normal force at the bottom wall, and F N 2 is the normal force at the vertical wall.
We can relate the angular acceleration to time and angular velocity, and since the final angular velocity is 0 , t = α ω 0 = r v ( μ r ( F N 1 + F N 2 ) I ) . The moment of inertia of a disk is simply I = 2 1 m r 2 , and we can obtain the normal forces by analyzing the forces acting on the spinning cylinder. We note that the spinning disk is not translating (in equilibrium), the net force is 0 . Thus, we can see that m g = μ F N 2 + F N 1 and F N 2 = μ F N 1 . We solve these two systems of equation to obtain F N 1 = μ 2 + 1 m g and F N 2 = μ 2 + 1 μ m g . Subbing this all into the equation we obtained for time, we get t = 2 g v μ ( 1 + μ ) μ 2 + 1 = 4 . 2 8
Resolving the forces acting on the cylinder along x & y-axes, we get, μ N x = N x & μ N y + N y = m g where, N x & N y a r e t h e n o r m a l f o r c e s a c t i n g o n t h e c y l i n d e r a l o n g x & y − a x e s r e s p e c t i v e l y d u e t o t h e w a l l s . A s t h e n e t t o r q u e a c t i n g a t t h e c o n t a c t s i s ( μ N x + μ N y ) r , g = 9 . 8 1 m / s 2 ( g i v e n ) , & t h e d e c e l e r a t i o n i s a = α ∗ r (where the notations denote their usual meanings) & s i n c e t h e m o m e n t o f i n e r t i a o f t h e c y l i n d e r i s ( m r 2 ) / 2 . Therefore on simplifying, we get a = 1 + μ 2 2 μ ( 1 + μ ) g which is surprisingly independent of both mass & radius. Applying, equations of classical Newtonian mechanics, v = u + a t where v = 0 , u = 3 0 m / s and substituting the calculated deceleration "a" (taking into account the negative sign), we can calculate the time required by the cylinder to stop rotating completely, yielding, T ⇒ 4 . 2 7 8 s .
Let N f and N w be the normal forces also F f and F w be the horizontal forces on the floor and wall respectively. Then,
Horizontal Force:
F f − N w = 0
Vertical Force:
F w + N f − m g = 0
Because F f = μ N f and F w = μ N w ,
Hence we get,
F f = 1 + μ 2 m g μ
F w = 1 + μ 2 m g μ 2
( F f + F w ) R θ = 2 1 I ω 2
θ = 2 g μ ( 1 + μ ) R ω 2 ( 1 + μ 2 )
Since θ = ω t and ω = R v substitute to the equation above as we get,
t = 2 g μ ( 1 + μ ) v ( 1 + μ 2 )
t = 2 × 9 . 8 1 × 0 . 3 × ( 1 + 0 . 3 ) 3 0 × ( 1 + 0 . 3 2 )
t = 4 . 2 7 3