Cylinders Intersecting In 3 Dimensions
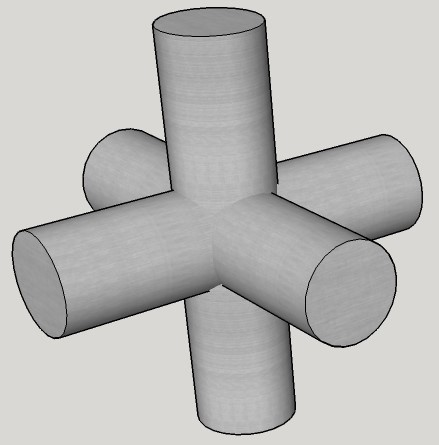
Three unit cylinders have axes on the , , and axes. What is the volume of their intersection?
Give your answer to 2 decimal places.
Note : Try this problem first.
The answer is 4.69.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The intersection of any two of these cylinders is two base-to-base "vaults", each of which has square cross sections. Here is the final intersection of all three cylinders:
Here is the final intersection of all three cylinders:
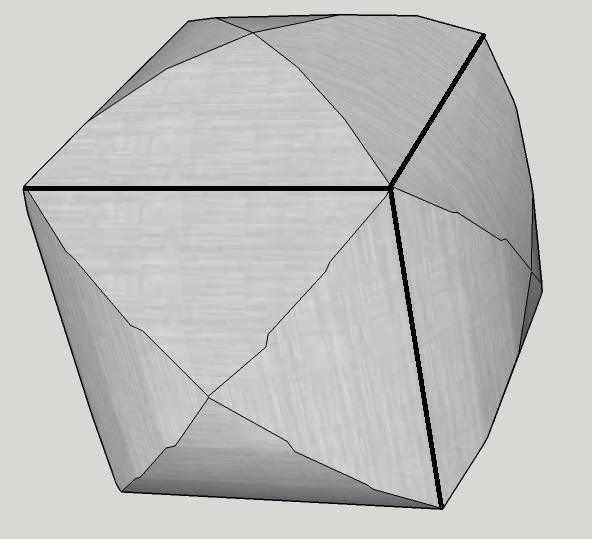 The easiest way to think of this shape is as a cube plus six partial vaults. The cube has face diagonal 2 (two radii of a unit cylinder), side length
2
, and volume
2
2
.
The easiest way to think of this shape is as a cube plus six partial vaults. The cube has face diagonal 2 (two radii of a unit cylinder), side length
2
, and volume
2
2
.
Each partial vault is bounded by the cube and by the surfaces of two of the cylinders. Its base (at the cube) is half the cube side length, or 2 / 2 , from the origin along the axis (call it z ) of the other cylinder. We'll slice the partial vault, so that for each value of z from 2 / 2 to 1 we have a square of side 2 1 − z 2 and area 4 ( 1 − z 2 ) . The volume of each partial vault, then, is: ∫ 2 / 2 1 4 ( 1 − z 2 ) d z = 4 [ 2 / 2 1 z − 3 z 3 ] = 3 8 − 5 2
So the total volume is: 2 2 + 6 ⋅ 3 8 − 5 2 = 8 ⋅ ( 2 − 2 ) ≈ 4 . 6 9