Cylindrical mirror
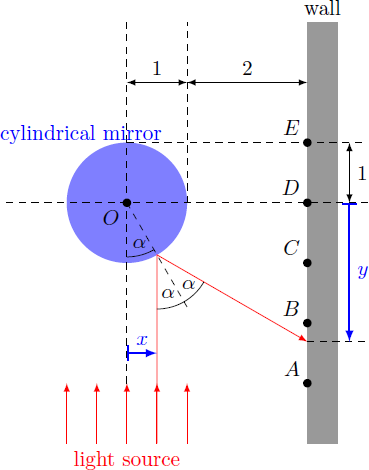
At the origin (point ) there is a reflecting cylinder with radius 1. From negative -direction the cylinder is illuminated by a homogeneous ligth source, so that the incident rays run parallel to the -axis. The light is reflected at the surface of the cylinder and hits a wall at . Which point on the wall is illuminated the brightest by the reflected light?
Hint: A ray of light striking the cylinder at a distance of to the -axis hits a certain point on the wall. Find the function that describes this reflection. The incident light is parallel and homogeneous, so that intensity on the wall is determined only by the function .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The light rays hit the cylinder at an angle α = arcsin x . The reflected beam then has an angle 2 α to the incident beam. The corresponding point on the wall then gives f ( x ) = y = − cos α − ( 3 − sin α ) cot 2 α = − cos α − ( 3 − sin α ) cos 2 α − sin 2 α 2 sin α cos α = − 1 − x 2 − ( 3 − x ) ( 1 − x 2 ) − x 2 2 x 1 − x 2 = 2 x 1 − x 2 6 x 2 − x − 3 This function has poles for the points x = 0 and x = 1 , so that the function value diverges here ( lim x → 0 f ( x ) = − ∞ , lim x → 1 f ( x ) = + ∞ ) . Physically these cases correspond to reflections with the angles α = 0 ∘ and 1 8 0 ∘ , so that the reflected rays run parallel to the wall. In the domain x ∈ ( 0 , 1 ) the function is well-behaved, so that we can calculate the derivative of the function f ( x ) results according to the quotient rule: f ′ ( x ) = ( 2 x 1 − x 2 ) 2 ( 1 2 x − 1 ) ⋅ ( 2 x 1 − x 2 ) − ( 6 x 2 − x − 3 ) ⋅ ( 2 1 − x 2 − 2 x 2 / 1 − x 2 ) = 2 x 2 ( 1 − x 2 ) 3 / 2 ( 1 2 x 2 − x ) ( 1 − x 2 ) − ( 6 x 2 − x − 3 ) ( 1 − 2 x 2 ) = 2 x 2 ( 1 − x 2 ) 3 / 2 ( − 1 2 x 4 + x 3 + 1 2 x 2 − x ) − ( − 1 2 x 4 + 2 x 3 + 1 2 x 2 − x − 3 ) = 2 x 2 ( 1 − x 2 ) 3 / 2 3 − x 3 For x ∈ ( 0 , 1 ) , the derivative f ′ ( x ) is positive, so that the function f ( x ) is monotone increasing. Therefore, the function can be inverted within the domain, so that each point y can be assigned a unique point x = f − 1 ( y ) . However, the inverse function can only be determined graphically or numerically so that we first plot the function and the derivative: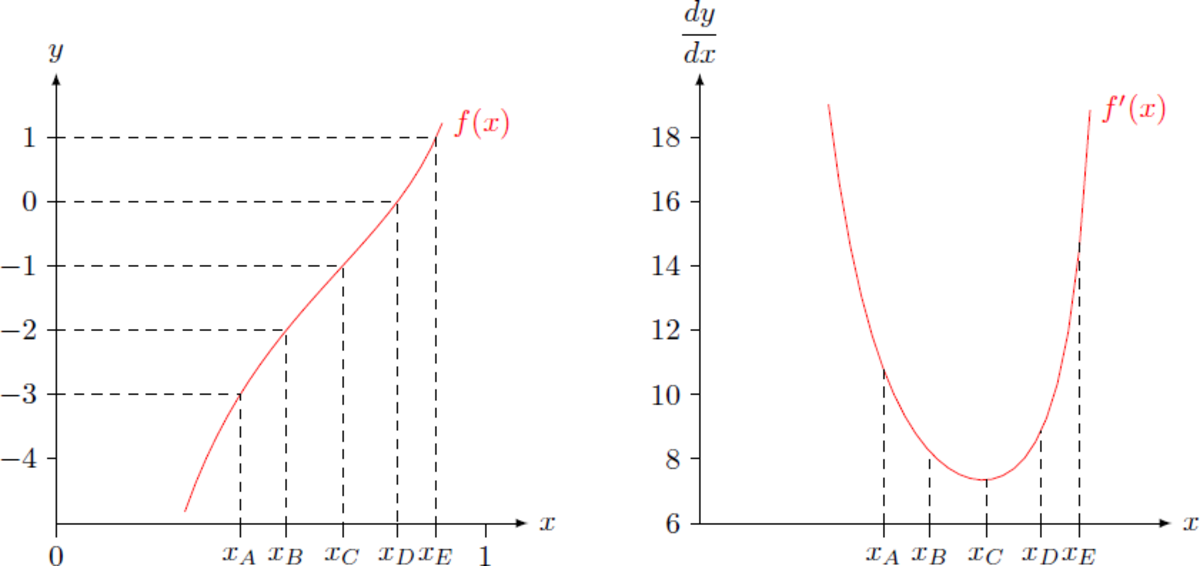 For the points
A
,
B
,
C
,
D
and
E
, which correspond to the function values
f
(
x
)
=
−
3
,
−
2
,
−
1
,
0
and
1
, the corresponding x-values and derivatives can be determined numerically:
x
A
x
B
x
C
x
D
x
E
=
f
−
1
(
−
3
)
≈
0
.
4
2
9
=
f
−
1
(
−
2
)
≈
0
.
5
3
6
=
f
−
1
(
−
1
)
≈
0
.
6
6
8
=
f
−
1
(
0
)
≈
0
.
7
9
5
=
f
−
1
(
1
)
≈
0
.
8
8
6
⇒
⇒
⇒
⇒
⇒
f
′
(
x
A
)
f
′
(
x
B
)
f
′
(
x
C
)
f
′
(
x
D
)
f
′
(
x
E
)
≈
1
0
.
7
7
≈
8
.
2
3
≈
7
.
3
5
≈
8
.
8
5
≈
1
4
.
7
2
It is noticeable, that the point
x
C
corresponds to the point of lowest slope. The slope
f
′
(
x
)
is a measure of how much the reflected rays diverge. Two rays, each incident at points
x
and
x
+
d
x
, strike the wall at points
f
(
x
)
and
f
(
x
)
+
f
′
(
x
)
d
x
, respectively. If the slope
f
′
(
x
)
is high, the rays diverge and the light intensity is small. If the slope
f
′
(
x
)
is small, then the rays are focused and the light intensity is large. Therefore, at point
C
, the highest light intensity will be observed.
For the points
A
,
B
,
C
,
D
and
E
, which correspond to the function values
f
(
x
)
=
−
3
,
−
2
,
−
1
,
0
and
1
, the corresponding x-values and derivatives can be determined numerically:
x
A
x
B
x
C
x
D
x
E
=
f
−
1
(
−
3
)
≈
0
.
4
2
9
=
f
−
1
(
−
2
)
≈
0
.
5
3
6
=
f
−
1
(
−
1
)
≈
0
.
6
6
8
=
f
−
1
(
0
)
≈
0
.
7
9
5
=
f
−
1
(
1
)
≈
0
.
8
8
6
⇒
⇒
⇒
⇒
⇒
f
′
(
x
A
)
f
′
(
x
B
)
f
′
(
x
C
)
f
′
(
x
D
)
f
′
(
x
E
)
≈
1
0
.
7
7
≈
8
.
2
3
≈
7
.
3
5
≈
8
.
8
5
≈
1
4
.
7
2
It is noticeable, that the point
x
C
corresponds to the point of lowest slope. The slope
f
′
(
x
)
is a measure of how much the reflected rays diverge. Two rays, each incident at points
x
and
x
+
d
x
, strike the wall at points
f
(
x
)
and
f
(
x
)
+
f
′
(
x
)
d
x
, respectively. If the slope
f
′
(
x
)
is high, the rays diverge and the light intensity is small. If the slope
f
′
(
x
)
is small, then the rays are focused and the light intensity is large. Therefore, at point
C
, the highest light intensity will be observed.