Damaged clock
A clock is made out of a disk of radius R = 1 0 cm which is hung by a point on its edge and oscillates. All of a sudden, a circular part right next to the hanging point of radius 2 R falls off, but the clock continues oscillating. What is the absolute value of the difference in s between the periods of oscillation before and after the part fell off?
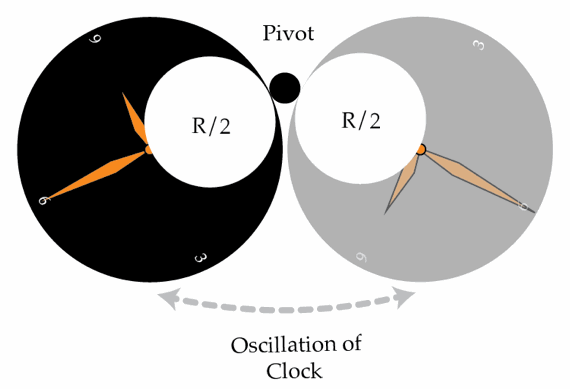
Details and assumptions
- Gravitational acceleration is g = 9 . 8 1 m/s 2
- Amplitude of the vertical oscillations is small
- The axis of rotation of the disc is horizontal all the time
- The disc is homogeneous
The answer is 0.027.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
We know that the period of a pendulum is 2 π m g R I . where I is the moment of inertia with respect to the axis of rotation, m is the mass of the clock, g = 9 . 8 1 is the acceleration due to gravity, and R is the distance from the fulcrum to the center of mass .
We know that the moment of inertia of a solid disk is 2 m r 2 , where r is the radius of the disk. However, this is not the moment of inertia we are looking for. We want the moment of inertia around the axis parallel but at a distance r away from the center.
By the parallel axis theorem , the moment of inertia of the disk around the fulcrum is 2 m r 2 + m r 2 = 2 3 m r 2 .
First, we calculate the period of the non-damaged clock. We already calculated I , which we know to be 2 3 m r 2 . The m in the numerator cancels out the m in the denominator. We know that g = 9 . 8 1 . The center of mass of a solid homogenous disk is at the center of a disk. Therefore, in this case, R = r = 0 . 1 .
Since we have all the information we need, we can plug numbers in to get that the period of the non-damaged clock is 0 . 7 7 7 3 4 .
In order to find the moment of inertia of the damaged clock, we subtract the moment of inertia of the broken piece from the moment of inertia of the undamaged clock. In this case, the moment of inertia of the broken piece is 2 3 ( 4 m ) ( 2 r ) 2 . We know this because the broken piece is similar to the non-damaged clock, except that it has been scaled down by a factor of 2 , which means that its mass, which is proportional to the square of the radius, is scaled down by a factor of 4 . The radius has also been scaled down by a factor of 2 . This means that the moment of inertia of the broken clock is 2 3 m r 2 − 2 3 ( 4 m ) ( 2 r ) 2 = 3 2 4 5 m r 2 .
The mass of the damaged clock is 4 3 the mass of the non-damaged clock, which means that m I for the damaged clock is ( 3 2 4 5 m r 2 ) ( 3 m 4 ) = 8 1 5 r 2 .
We know that the center of mass of the broken piece is 2 r from the center of the clock towards the fulcrum, and that the broken piece is 3 1 the mass of the damaged clock. In order to make up for the missing mass, the center of mass of the damaged clock is 6 r from the center of the clock away from the fulcrum, which means that it is 6 7 r from the fulcrum. Therefore, R = 6 7 r for the damaged clock.
Since we have m I , g , and R for the damaged clock, we can plug numbers in to get that the period of the damaged clock is 0 . 8 0 4 6 3 .
The difference between the periods is 0 . 0 2 7 3 .
The small-angle approximation for the period of a compound pendulum is T ≈ 2 π m g R C M I , where I is the moment of inertia about the axis of rotation and R C M is the distance from the axis of rotation to the center of mass of the pendulum. Since the disk is homogenous, it has some uniform areal mass density σ . Let's say that a circular pendulum of radius R has the polar form r = − 2 R sin θ for 0 ≤ θ ≤ π . The mass m i of this pendulum is π R 2 σ , and its center of mass lies at ( 0 , − R ) , so R C M , i = R . The moments of inertia are defined as ( I x , I y ) = ∫ V r 2 σ d V = ∫ V ( r 2 σ cos 2 t , r 2 σ sin 2 t ) d V . We rewrite d V as r d r d θ and evaluate to get I P , i = I x + I y = 2 3 π R 4 σ . Thus, the initial period T i of the pendulum is 2 π 2 ( π g R 2 R σ ) 3 π R 4 σ = π g 6 R .
Now, we calculate the same quantities for the second pendulum. The mass m f is equal to m i minus the mass Δ m of the missing piece [which we may find to be π ( 2 R ) 2 σ , so m f = 4 3 π R 2 σ . The center of mass of this new pendulum is m f m i R C M , i + Δ m R C M , m i s s i n g = ( 0 , 6 − 7 R ) , so R C M , f = 6 7 R . Also, the moment of inertia calculation is the same except for the lower d r bound, which becomes − R sin θ . Incidentally, I P , f = 3 2 4 5 π R 4 σ . These quantities provide a period T f = 2 π 4 3 π R 2 σ g ( 6 7 R ) 3 2 4 5 π R 4 σ = π 7 g 4 5 R . After plugging in 9 . 8 1 m / s 2 for g and 1 0 cm for R and converting to the right units, we get that the difference between T f and T i is ≈ 0 . 0 2 7 3 s .
Well, we are told that we can think of the clock as a circumference with uniform surface density σ . This clock is a rigid body oscillating freely about an axis, and that's what we call a Physical Pendulum.
So, the analysis involves the moment of inertia I of the clock about some axis and the distance from the pivot to the center of mass r . The period of oscillation of such a pendulum is given by:
T = 2 π m g r I
Where m is the mass of the pendulum, in this case the clock. The moment of inertia of a thin disk about an axis perpendicular to the surface with the pivot at the center, mass m and radius r is 2 1 m r 2 and by the parallel axis theorem, we find that the moment of inertia, under the conditions, of the initial clock is I = 2 3 m r 2 .
Now, there are two situations to analyze, the motion of the clock normally, and the motion of the clock with the hole.
The moment of inertia in the first case is I 1 = 2 3 m R 2 .
For the second case we must remember that the moment of inertia is found by adding all the contributions from each piece of the clock, so, if part of the clock disappears, we just have to subtract the contribution due to that part I p .
The mass of the piece m p = σ ∗ A r e a = σ ∗ π ∗ ( 2 R ) 2 = 4 m , so the small piece contains a fourth of the mass of the initial clock, so it's contribution to the moment of inertia of the initial clock is I p = 2 3 ( 4 m ) ( 2 R ) 2 = 4 1 4 1 2 3 m R 2 = 1 6 1 I 1 .
We can finally say that the moment of inertia of the modified clock under the conditions is I 2 = I 1 − I p = 1 6 1 5 I 1
Now we just must find the distances r in each situation.
In the first situation, I think it's clear that the center of the mass of the clock is located at the center (by symmetry), so the distance from the pivot to the center of mass is r 1 = R .
For the second situation, we must deal with something similar to the moment of inertia case. We know that the small piece has mass 4 m , and the distance from it's center of mass to the pivot is 2 R . Therefore we know that the mass of the rest of the clock is 4 3 m . We already know where the center of mass of the total clock is, so the next equation must hold: ( 4 m ) ( 2 R ) + ( 4 3 m ) r 2 = m R so that it's located at a distance R from the pivot point. Therefore r 2 is the distance from the pivot point to the center of mass of the clock with the hole. Easily we find that r 2 = 6 7 R and FINALLY we have all we need to find the answer t = ∣ T 1 − T 2 ∣ . Notice that the mass m in the equation of T cancels with the one in I .
Playing a bit with T 1 a n d T 2 , or just by replacing, we can finally find:
t = T 2 − T 1 = T 1 ( 1 4 1 5 − 1 ) = 2 π 9 . 8 1 m / s 2 ∗ 0 . 1 m 0 . 0 1 5 m 2 = 0 . 0 2 7 3 s
the formula is given by: T=2\pi\sqrt{\frac{I}{mgd}} where I is the moment of inertia with respect to the hanging point, m is the mass of the pendulum and d is the distance from the center of mass to the hanging point. Before the part fell off: T {1}= 2\pi\sqrt{\frac{3R}{2g}} = 0.7769s After the part fell off: (assume the mass per unit area is k) The new moment of inertia: I {new}=I {whole clock} - I {falling part} = \frac{3}{2}k\piR^2 R^2 - \frac{3}{2}k\pi (R/2)^4 The new parameter md: md {new}= md {whole clock} - md {falling part} = k\pi*R^2*R - k\pi*(R/2)^3 Apply the formula of period we obtain that T {2}= 2\pi\sqrt{\frac{R}{g}}\sqrt{\frac{45}{28}} = 0.804s Therefore, T {2} - T {1} = 0.0273s
Let the torque around the axis of rotation be Tq1 and Tq2 before and after the smaller disk falls off, and the moment of inertia I1 and I2, respectively.
Tq1= mgRsinA, where A is the small angular displacement from the vertical line of reference. With linear approximation sinA=A for A<<1, Tq1=mgRA. And I1 = (3/2) mR^2.
After the disk falls off, the new center of mass is R+(1/3)(1/2)R = (7/6)R from the axis of rotation. Hence Tq2=(3/4)mg(7R/6)sinA=(7/8)mgRA. And I2=(3/2)[mR^2-(m/4)(R/2)^2]=(45/32)mR^2.
Therefore, A''(t)= -Tq/I= -w^2 A; w1=srqt[2g/(3R)], w2=sqrt[28g/(45R)].
This yields: T1=(2x3.14)sqrt[3R/(2g)], and T2=(2x3.14)sqrt[45R/(28g)]. |T2-T1| = 0.027
The period of a compound pendulum is given by
T = 2 π m g d I
T is the period, I is the moment of inertia with respect to the pivot, m is the mass of the pendulum d is the distance from the centre of mass to the pivot.
The moment of inertia of the undamaged pendulum is simply found using the parallel axis theorem.
I u = 2 M R 2 + M R 2 = 2 3 M R 2
For the damaged clock the moment of inertia is the moment of inertia of the large disk minus the small disk.
I s m a l l d i s k = 2 3 4 M ( 2 R ) 2 = 3 2 3 M R 2
I d = I u − I s m a l l d i s k = 3 2 4 5 M R 2
The position of the center of mass of the damaged clock has also shifted. With respect to the center of the small disk,
x d a m a g e d = 4 3 M − 4 M 2 R = − 6 R
so d for the damaged clock is 6 7 R
Therefore, the change in period is
δ T = 2 π 0 . 7 5 M g 6 7 R I d − 2 π M g R I u
After alot of substitution ( R = 0 . 1 0 m , g = 9 . 8 m s − 2 mass is not needed as it cancels out ), we get 0.0273 seconds.
The rotation of a physical pendulum is governed by the second Newton's law for rotational motion: I α = − m g l where I is the moment of inertia with respect to the axis of oscillations, α is the angular acceleration, m is the total pendulum's mass and l is the distance of the center of mass from the axis or rotation. Therefore, we can derive the frequency of oscillation as ω = I m g l .
Therefore, in this problem we need to find the distance from the center of mass before and after, and moment of inertia before and after the circular part fell off.
Before: Center of mass is in the middle of the disc, l 1 = R . Moment of inertia is equal to the sum of the moment of inertia of a disc rotating around its center ( 0 . 5 M R 2 ) and the correction due to the parallel axis theorem: I 1 = 0 . 5 M R 2 + M R 2 . Therefore, the period of oscillations before the breaking was T 1 = 2 π M g R 1 . 5 M R 2 = 2 π g 1 . 5 R = 0 . 7 7 7 s .
After: Center of the mass is given by l 2 = M − m M R − 0 . 5 m R . Since the disc is homogeneous, the density is constant everywhere, so R 2 M = 0 . 2 5 R 2 m , and m = 0 . 2 5 M is the missing mass. Therefore, l 2 = 1 . 1 6 7 R .
Moment of inertia can be found by superimposing the full disc and a small disc of a "negative" mass 0 . 2 5 M : I 2 = ( 0 . 5 M R 2 + M R 2 ) − ( 0 . 5 m ( 0 . 5 R ) 2 + m ( 0 . 5 R ) 2 ) = 1 . 4 0 6 M R 2 . The period of oscillation is T 2 = 2 π 0 . 7 5 M g × 1 . 1 6 7 R 1 . 4 0 6 M R 2 = 2 π g 1 . 6 0 6 R = 0 . 8 0 4 s .
Therefore, the difference in the period of oscillations is T 1 − T 2 = − 0 . 0 2 7 s .
Thats a nice problem, at first i didnt consider that the distance between the pivot , and the center of mass changes ,then I did pay attention and found out the solution
The equation of motion is provided by the rotational variant of F = m a , namely, τ = I θ ¨ , where τ is the torque provided by gravity, I is the moment of inertia of the clock and θ is the angle of the clock, which I define to be the angle between the vertical and the line through the pivot and the center of the clock.
The moment of inertia of a homogeneous disk of mass m and radius r is I = 2 1 m r 2 , if the rotation axis were at the center. By the parallel axis theorem, if the axis is a distance l away from the center, the moment of inertia increases by m l 2 . In conclusion, the moment of inertia of the clock is I = 2 1 m R 2 + m R 2 = 2 3 m R 2 , where m is the (unknown) mass of the clock.
The torque (on a point mass) is τ = r × F , where r is the vector from the pivot to the point. To determine the total torque on the clock, we need to integrate. The gravitational force on an infinetismal area d A is − ρ g z ^ , where ρ is the mass density. This gives us
τ = ∫ d A r ′ × − ρ g z ^ = g z ^ × ∫ d A ρ r ′ = g z ^ × m r c m ,
where r c m is the center of mass of the disk, which is trivially at the center of the disk. Hence ∣ τ ∣ = m g R sin θ , since θ is (by definition) the angle between r c m and z ^ .
The equation of motion τ = I θ ¨ thus turns into
2 3 m R 2 θ ¨ = − m g R sin θ ,
where the minus sign accounts for the fact that the force is always directed opposite to the direction of θ . This differential equation cannot be solved exactly, but analogous to the standard ideal pendulum, we use the assumption that the amplitude of oscillation is small to approximate sin θ ≈ θ , which ultimately yields the solution
θ ( t ) = A cos ( ω t + ϕ ) ,
where ω = 2 3 m R 2 m g R = I m g r c m = 3 R 2 g , and A and ϕ are free parameters (to be fixed by initial conditions). The oscillation period is thus
T = ω 2 π = 2 π m g r c m I = 2 π 2 g 3 R .
For the clock with the missing part, m , I and r c m are all different. I will use primed variables to refer to the clock with the missing part, and tildes to refer to the missing part itself. First off, trivially we have m ~ = 4 1 m and hence m ′ = 4 3 m .
The moment of inertia of the missing part is, analogous to before, I ~ = 2 3 m ~ ( R / 2 ) 2 = 1 6 1 I . Since moments of inertia are additive, we have I ′ = I − I ~ = 1 6 1 5 I .
Finally, the rule for combining centers of mass tells us m r c m = m ′ r c m ′ + m ~ r ~ c m . We easily find r ~ c m = R / 2 , hence m R = 4 3 m r c m ′ + 8 1 m R , which solves to r c m ′ = 6 7 R .
Proceeding as before we find
T ′ = 2 π m ′ g r c m ′ I ′ = 2 π ( 3 / 4 ) m g ( 7 / 6 ) r c m ( 1 5 / 1 6 ) I = 1 6 1 5 ⋅ 3 4 ⋅ 7 6 ⋅ 2 π m g r c m I = 1 4 1 5 T .
The requested difference in time is thus Δ T = T ′ − T = 2 π 2 g 3 R ( 1 4 1 5 − 1 ) = 0 . 0 2 7 s .