Stronger than Classical Inequalities!
Let a , b , and c be real numbers such that 0 ≤ a , b , c ≤ 2 1 and a + b + c = 1 . Find the maximum value of
a 3 + b 3 + c 3 + 4 a b c
The answer is 0.28125.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
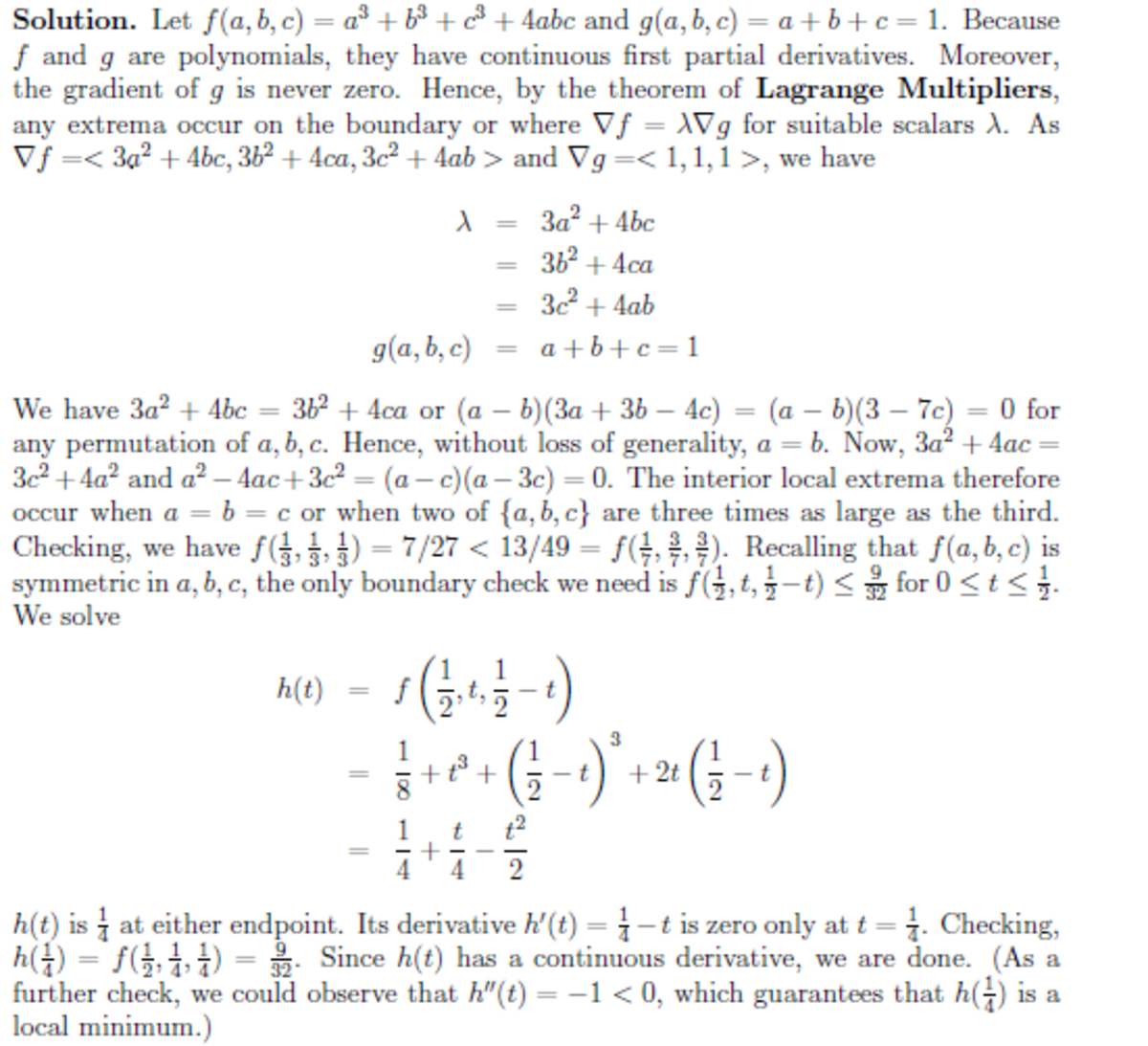
Nice solution. After substituting c = 1 - a - b, the inequalities became 0<=a,b<=1/2 and a+b>=1/2. I had a hunch that I only needed to check the three boundaries (actually only two because two were identical w.r.t the problem) of the 2-D inequalities. I thought about trying Lagrange multipliers, but I guess I was just lazy. I was more interested in finding an algebra solution. I never found one. But I wonder if it can be easily justified that all you need to do is check the boundary.
f ( a , b , c ) = a 3 + b 3 + c 3 + 4 ∗ a ∗ b ∗ c . f ( 1 / 2 , 0 , 1 / 2 ) = . 2 5 . f ( 1 / 3 , 1 / 3 , 1 / 3 ) = . 2 5 9 2 5 9 2 5 9 . . . . . f ( 1 / 2 , 1 / 3 , 1 / 6 ) = . 2 7 7 7 7 7 . . . f ( 1 / 2 , 1 / 4 , 1 / 4 ) = . 2 8 1 2 A l l p o s s i b l e p a t t e r n s h a s b e e n i n v e s t i g a t e d . S o f o r t h e g i v e n c o n d i t i o n s , m a x i m u m p o s s i b l e v a l u e s a r e g i v e n t o a , b , c , t h a t r e t u r n s f m a x = . 2 8 1 2 5 . M a x v a l u e i s g i v e n t o a = 1 / 2 . M a x p o s s i b l e v a l u e s t o b a n d c c a n o n l y b e 1 / 4 s o t h a t n o n e g e t s s m a l l v a l u e .