Damped Orbit
There is a particle of mass M = 1 0 kg held in place at the origin of the x y plane. Another particle of mass m = 1 kg orbits the first particle. The force on the orbiting particle is:
F = F g − 0 . 1 v
In the above equation, F g is the gravitational force from the particle at the origin, and v is the velocity of the orbiting particle. The universal gravitational constant G = 1 .
At time t = 0 , the position and velocity are:
( x , y ) ( x ˙ , y ˙ ) = = ( 1 , 0 ) ( 0 , 1 0 )
At what time is the orbiting particle a distance of 0 . 2 away from the origin? If there are multiple times, give the earliest one.
The answer is 7.8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice solution sir
Thank you very much for sharing these insights
This problem was fun to solve. The method using which I obtained the answer can be studied in a commented script of code attached below. Also attached are some plots:
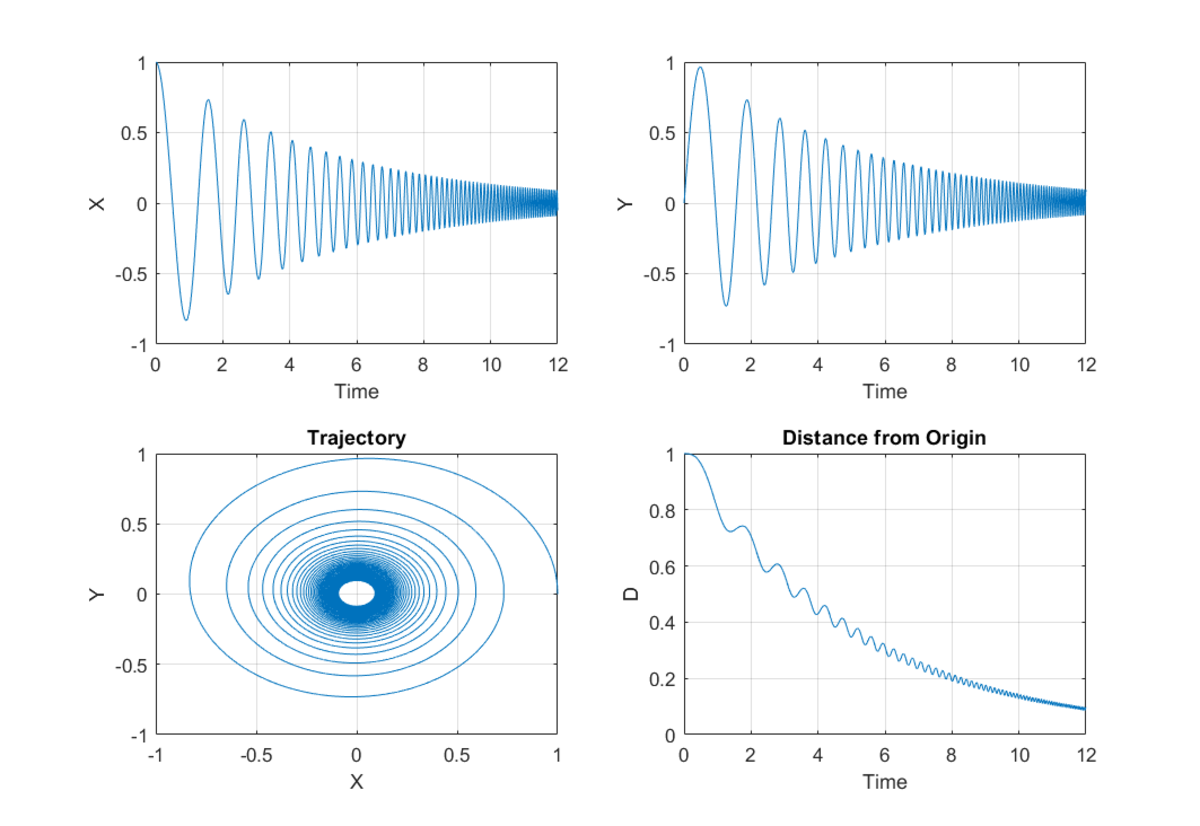
Compare the above to the case where no damping is present:
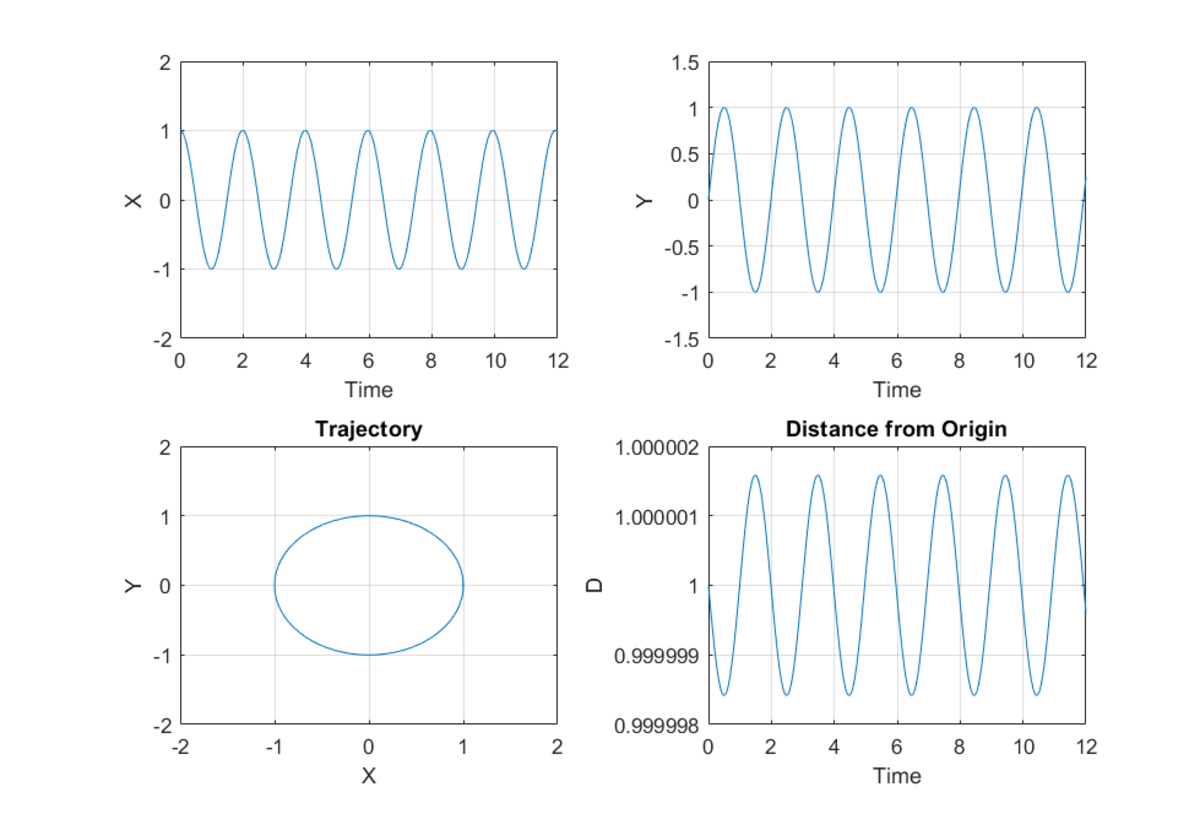
So basically, the damping results in a reduction of speed which results in a progressive reduction of orbital radius with time. In the absence of damping, we get the classical solution of the two body problem. The script used to generate plots is different from that used to find the result of this problem. In the latter, I ran a simulation until t = 1 2 .
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
|
@Karan Chatrath Your views on anayltical solution,??
Can we solve it?
Log in to reply
I don't know how to derive a closed form solution to this problem
Log in to reply
See my solution for how far we can go. There is a nice time-dependent expression for the angular momentum of the system, but the equation relating r and θ has an intractible time-dependent term.
The system of three equations to solve, where r(t) is the distance of the orbiting particle from the origin:
G = 1 , m 1 = 1 , m 2 = 1 0
m 1 x ′ ′ ( t ) = − ( x ( t ) 2 + y ( t ) 2 ) 3 / 2 G ( m 1 m 2 x ( t ) ) − 0 . 1 x ′ ( t )
m 1 y ′ ′ ( t ) = − ( x ( t ) 2 + y ( t ) 2 ) 3 / 2 G ( m 1 m 2 y ( t ) ) − 0 . 1 y ′ ( t )
r ( t ) = x ( t ) 2 + y ( t ) 2
Solved it digitally using Wolfram. Here is a plot of the solution for x(t), y(t) and r(t) vs time:
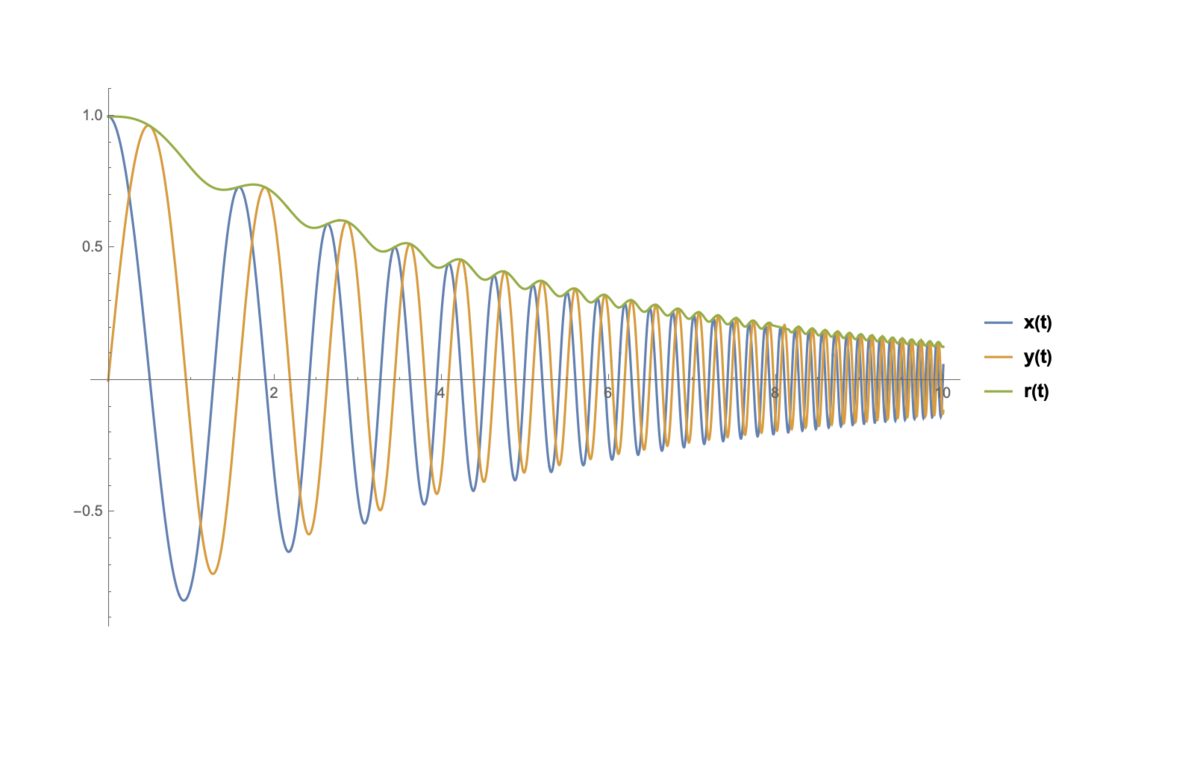
If we introduce polar coordinates and consider the radial and transverse equations of motion, we obtain the equations r ¨ − r θ ˙ 2 = − 1 0 r − 2 − 1 0 1 r ˙ 2 r ˙ θ ˙ + r θ ¨ = − 1 0 1 r θ ˙ The second of these simplifies to read d t d ( r 2 θ ˙ e 1 0 1 t ) = 0 and hence, given then initial conditions, we deduce that r 2 θ ˙ = 1 0 e − 1 0 1 t so we see that the angular momentum of the system decays exponentially with time. We can now substitute for θ ˙ in the radial equation, obtaining r ¨ − 1 0 r − 3 e − 5 1 t + 1 0 r − 2 + 1 0 1 r ˙ = 0 If we attempt the usual substitution u = r − 1 at this stage, we obtain the equation d θ 2 d 2 u + u = e 5 1 t This is elegant, but not easy to solve, so we revert to solving the differentiaL equation r ¨ − 1 0 r − 3 e − 5 1 t + 1 0 r − 2 + 1 0 1 r ˙ = 0 together with the initial conditions r ( 0 ) = 1 and r ˙ ( 0 ) = 0 , numerically. A plot of the first 8 seconds is below:
There are three times in the first 8 seconds when the radius reaches the value of 0 . 2 , namely t = 7 . 8 0 3 3 3 6 , t = 7 . 8 4 3 8 9 6 and t = 7 . 9 7 2 0 1 6 .