Damped Oscillation 12-4-2020
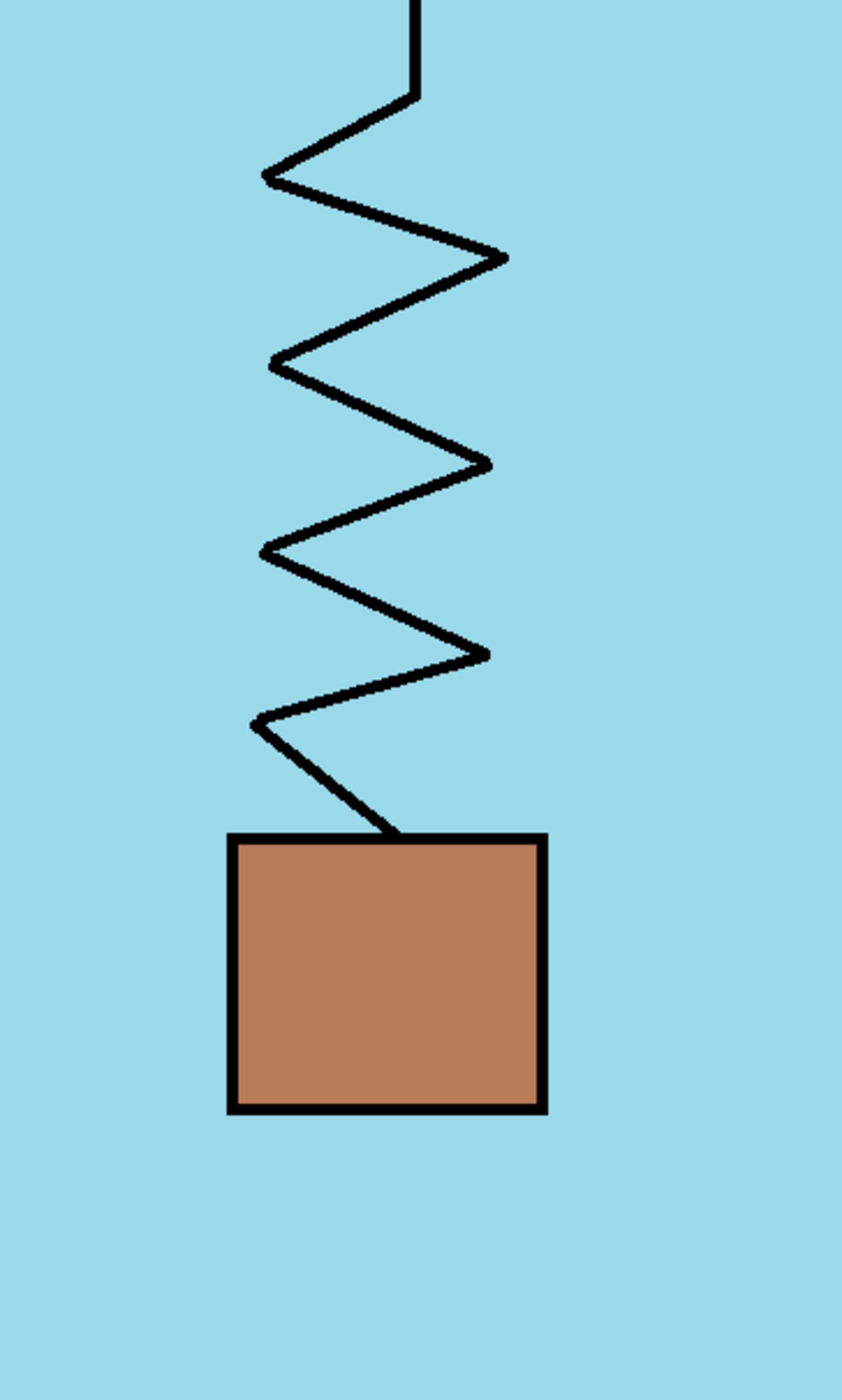
A mass is connected to one end of a spring of force constant . The other end of the spring is fixed in place. At time , the spring is at its natural length, and the mass is at rest at position . The ambient gravitational acceleration is downward, which corresponds to the direction. As the mass moves, it is subjected to damping forces, such that the differential equation describing its motion is:
What is the position of the mass at time ?
Details and Assumptions:
1)
2)
3)
4)
5)
Assume standard
units for all quantities
The answer is 2.337.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Substituting the given parameters in the given differential equation, we obtain,
y ¨ + 0 . 5 y ˙ + 5 y = 1 0
Taking the Laplace transform of the both sides, and keeping in mind that y ( 0 ) = y ˙ ( 0 ) = 0 ,
s 2 Y ( s ) + 0 . 5 s Y ( s ) + 5 Y ( s ) = s 1 0
So that,
Y ( s ) = s ( s 2 + 0 . 5 s + 5 ) 1 0 = s ( ( s + a ) 2 + b 2 ) 1 0
where a = 0 . 2 5 , b 2 = 5 − a 2
Using partial fractions, Y ( s ) can be expressed as follows:
Y ( s ) = s ( ( s + a ) 2 + b 2 ) 1 0 = s A + ( s + a ) 2 + b 2 B ( s + a ) + ( s + a ) 2 + b 2 C b
And this means that,
1 0 = A ( ( s + a ) 2 + b 2 ) + B s ( s + a ) + C b s
Equating equal powers of s on both sides of the equation, we deduce that,
0 = A + B
0 = 2 A a + B a + C b
1 0 = A ( a 2 + b 2 )
Hence,
A = a 2 + b 2 1 0
B = − a 2 + b 2 1 0
C = − b a ( 2 A + B ) = − b ( a 2 + b 2 ) 1 0 a
Finally, we Laplace invert the partial fraction expansion of Y ( s ) , to get,
y ( t ) = A + B e − a t cos ( b t ) + C e − a t sin ( b t )
Using the values of a , b , we find that A = 2 , B = − 2 , C = − 0 . 2 2 5 0 1 7 5 8 , hence, substituting t = 7 , we get,
y ( 7 ) ≈ 2 . 3 3 7