Damped oscillations

Classical Mechanics Level 4

Suppose I have an oscillating system, that oscillates under a standard restoring force given by :

F = − k x , F=-kx,

where x x is the displacement and k k is the constant of proportionality with k > 0 k > 0 .

Now suppose it is being damped by a viscous force given by the standard equation of

− b x ˙ = F d r a g . -b\dot { x } ={ F }_{ drag }.

Suppose that the particle under the forces have mass m m , and at t = 0 t = 0 we have x = x 0 x={ x }_{ 0 } .
Then what is the limiting value of b b for which the particle will not cross the origin even once?

Details and Assumptions

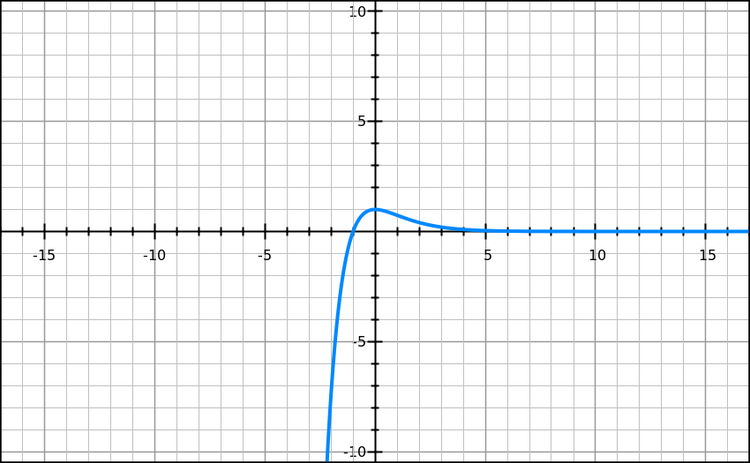
  • The graph of the particle will appear as shown.
  • Only consider the positive side, x-axis is time and y-axis displacement
  • m=1 kg
  • K=1 N/m
  • No driving force acts on the object.


The answer is 2.

Mvs Saketh by Mvs Saketh , 24, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Pranjal Jain
Dec 10, 2014

F = m x ′ ′ = − k x − b x ′ F=mx''=-kx-bx'

Solving this second order linear ODE, we get x ( t ) = c 1 e − t ( b 2 − 4 m k + b ) 2 m + c 2 e t ( b 2 − 4 m k − b ) 2 m x(t)=c_{1}e^{-\dfrac{t(\sqrt{b^{2}-4mk}+b)}{2m}}+c_{2}e^{\dfrac{t(\sqrt{b^{2}-4mk}-b)}{2m}}

For the limiting case of not crossing origin, b 2 − 4 m k = 0 b^{2}-4mk=0 or b = 2 b=2

8 Helpful 0 Interesting 0 Brilliant 0 Confused

Exactly , Because when b falls below 2, we get sinusoidal damped solutions (considering the real class of solutions) which necessarily cross the origin. It is interesting how it oscillates infinite times if b slightly less than 2 and just once when more or equal. Such a harsh discontinuity

Mvs Saketh - 6 years, 6 months ago

Log in to reply

Yeah! Thats somewhat cool!

Pranjal Jain - 6 years, 6 months ago

Can you tell how you solved it I am stuck

Ashwin Gopal - 6 years, 6 months ago

Log in to reply

You don't solve . You guess the solution.If you cannot access the videos reply here.

https://www.youtube.com/watch?v=f8HJ6g1S6OA

https://www.youtube.com/watch?v=XCdPk1pIT1Y

https://www.youtube.com/watch?v=NU5nkbOa1zk

https://www.youtube.com/watch?v=17D4U_r6Gwk

https://www.youtube.com/watch?v=LmFGrx-MSzU

If you want to learn more about Waves and Optics enroll in PHYS201x on EdX.

Arif Ahmed - 6 years, 5 months ago

what do you mean by ODE ? Does This equation has Many Other Solution also ? If So then what is Best Solution for This . ?

I just Use The Standard Solution of this Damping which is given in NCERT, x ( t ) = A 0 e − b t m sin ⁡ ( ω d t + ϕ ) ω d = ( k m ) − ( b 2 m ) 2 \displaystyle{x(t)={ A }_{ 0 }{ e }^{ \cfrac { -bt }{ m } }\sin { { (\omega }_{ d }t+\phi ) } \\ { \omega }_{ d }=\sqrt { { (\cfrac { k }{ m } ) }-{ (\cfrac { b }{ 2m } })^{ 2 } } }

Now For Never crossing X-axis It's Sinusoidal Time Phase Should be constant , Which is only Possible when It's damping frequency should be zero . (or Time period is Infinite) i.e ω d = 0 ⇒ b = 4 m k \displaystyle{{ \omega }_{ d }=0\quad \Rightarrow \boxed { b=\sqrt { 4mk } } }

Deepanshu Gupta - 6 years, 4 months ago

Log in to reply

ODE is ordinary differential equation,

yes, inface ur eqn holds when b is less than 2, when equal, another equation holds whose graph i have plotted. when more than 2, still another set of equations hold,, all solutions are however expressible as

C1e^(tr1)+C2e^(tr2) ,

ur way holds when r1 and r2 are imaginary and C1 = C2 (the good form) , then use e^(ix)=cos(x)+isin(x),

Mvs Saketh - 6 years, 4 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...