Damped Pendulum
A pendulum consists of a rigid massless rod of length L with one end hinged at the origin of the x y plane. The other end is connected to a ball of mass m . The pendulum rotates in the x y plane, and the ambient gravitational acceleration g is in the negative y direction.
There is also a damping force on the ball, which has the following form:
F D = − D v
In the above equation, D is a damping coefficient, and v is the velocity of the ball. At time t = 0 , the pendulum has zero speed and makes an angle θ with the positive x axis, as shown in the diagram.
At time t = 3 0 , what is the sum of the x and y coordinates of the ball?
Details and Assumptions:
1)
m
=
L
=
1
2)
g
=
1
0
3)
D
=
0
.
1
4)
θ
=
π
/
3
5)
The ball can be treated as a point particle
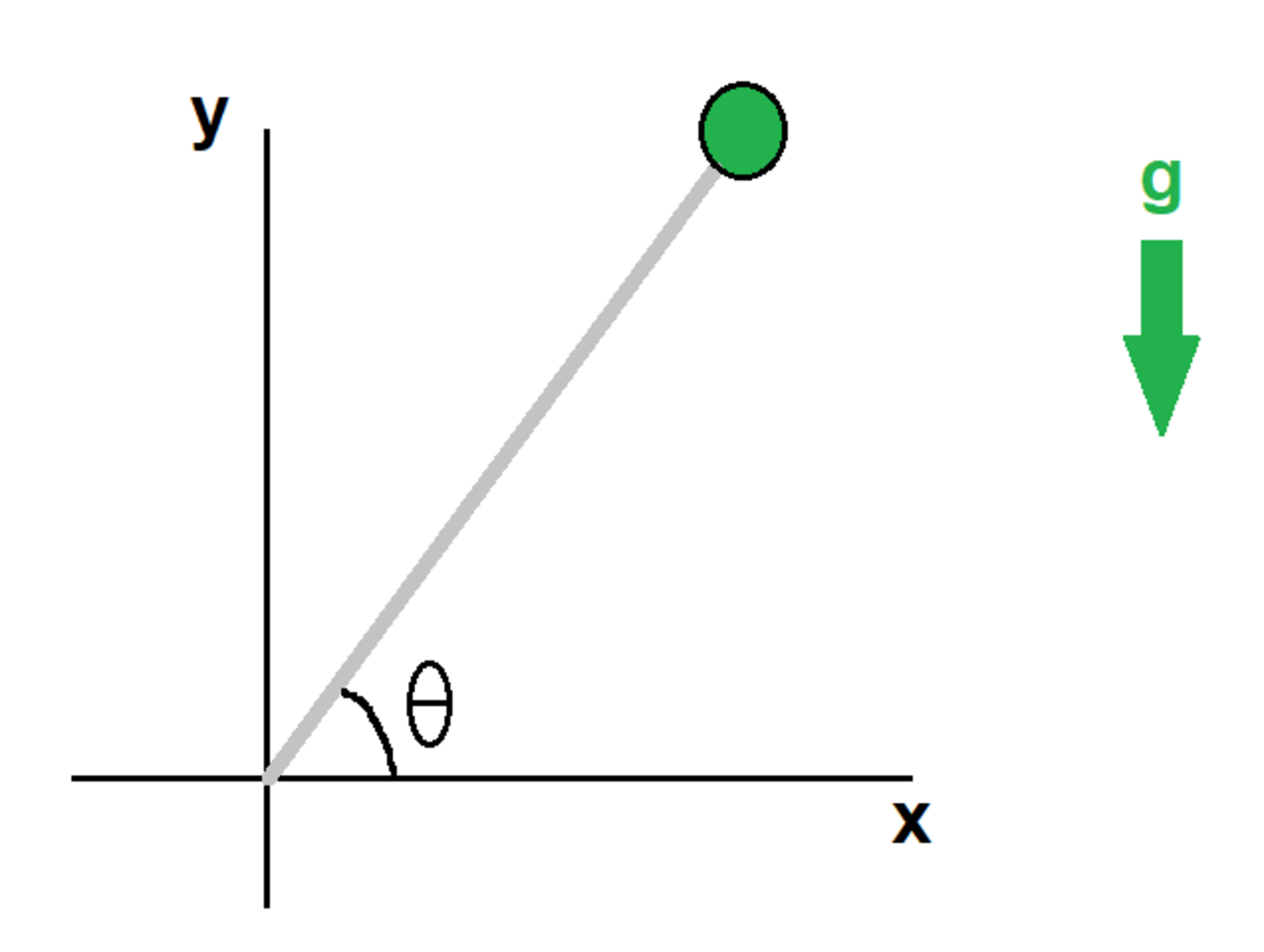
The answer is -1.344.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Karan Chatrath nice question.
I think it is interesting how @Karan Chatrath incorporated the rod tension into his solution. My approach was a bit more conventional.
Moment of Inertia:
I = m L 2
Position and velocity:
x = L cos θ y = L sin θ x ˙ = − L sin θ θ ˙ y ˙ = L cos θ θ ˙
Gravity, damping, and total force:
F g = ( 0 , − m g ) F D = ( − D x ˙ , − D y ˙ ) F = F g + F D
Torque from vector cross product:
r = ( x , y ) τ = r × F
The torque is one-dimensional, so it can be thought of as a scalar τ . The sign of τ changes appropriately to yield oscillation. Angular acceleration:
θ ¨ = I τ
Numerical integration takes care of the rest
At a general time t , let the coordinates of the ball be ( x , y ) = ( cos θ , sin θ ) . The velocity and acceleration components are:
[ x y ] = [ cos θ sin θ ] ⟹ [ x ˙ y ˙ ] = [ − θ ˙ sin θ θ ˙ cos θ ] ⟹ [ x ¨ y ¨ ] = [ − θ ¨ sin θ − θ ˙ 2 cos θ θ ¨ cos θ − θ ˙ 2 sin θ ]
Let the magnitude of tension be T and it is directed towards the origin along the length of the rod. Now, applying Newton's second law gives:
m [ x ¨ y ¨ ] = [ 0 − m g ] − T [ cos θ sin θ ] − D [ x ˙ y ˙ ]
This gives us a system of two equations in θ ¨ and T . Eliminating T from these set of equations leads to the final equation of motion which is the following. Simplifications left out.
θ ¨ = − 1 0 θ ˙ − 1 0 cos θ ; θ ( 0 ) = 3 π ; θ ˙ ( 0 ) = 0
We asked to compute the sum cos θ + sin θ at time t = 3 0 . This has been done numerically as follows: