Damped Vibrations
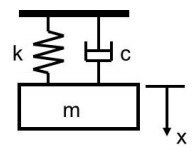
Consider a simple spring-mass-damper system as shown in the figure. One end of the spring and damper is fixed to a wall while the other is fixed to a body of mass . In this question, the effect of gravity is ignored.
The mass is given a massive displacement of downward (from its equilibrium position) and released from rest at time . The goal of the question is to compute the rate at which the system loses energy. Enter your answer as the magnitude of the rate of total energy loss of the system in at time seconds.
Bonus 1: Is the system over, under or critically damped? Why?
Bonus 2: If the value of the damping coefficient happened to be negative, how would one interpret the situation physically? Is such a situation possible in reality?
Note: The damping force is the product of the damping coefficient and the instantaneous velocity of the mass. Its direction is opposite to that of the velocity of the mass. The spring is linear and obeys Hooke's law.
The answer is 17.4981.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
I will briefly lay out the steps of the problem.
Differentiating the energy with respect to time: d t d E = x ˙ ( k x + M x ¨ ) .
We know that: M x ¨ + c x ˙ + k x = 0 . This implies: M x ¨ + k x = − c x ˙
Replacing the above result in the 'rate of energy change' equation gives us: d t d E = − c x ˙ 2
I am, for now, refraining to answer the bonus questions posed. These are conceptual questions worth thinking about.