Dancing top
A top of mass
m
=
0
.
5
kg
rotates with angular speed
ω
=
3
5
0
rad/s
around its axis which is tilted by a (constant) angle of
θ
=
4
5
∘
as shown in the figure. The moment of inertia with respect to the top's axis is
I
=
2
g
⋅
m
2
and the distance from the tip of the top to the center of mass is
l
=
1
0
cm
.
Determine the force of friction
f
in Newtons
acting on the tip of the top.
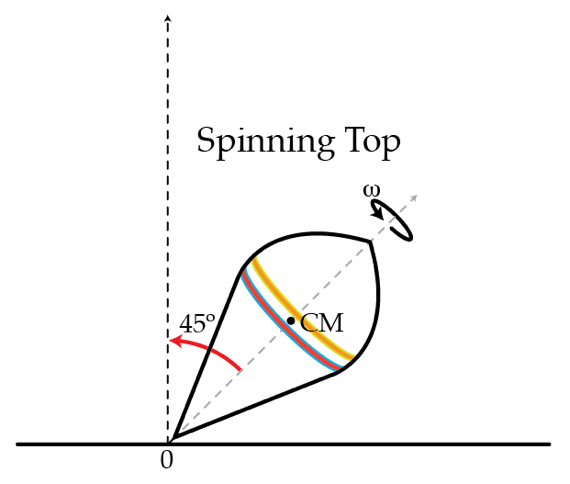
The answer is 0.0173.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
For the last sentence, we're subbing in for Ω , not ω (sorry, a typo).
nice solution.
First, let us note that,
-
Δ t i m e Δ A n g u l a r M o m e n t u m = t o r q u e
-
The length of an arc is equal to the radius of the circle times the subtending angle.
Since we are only given information about the top spinning around the rotated axis, let us relate that to the angular velocity of precession.
The vector I ∗ ω ∗ s i n ( 4 5 ∘ ) is on the plane containing the precession of the top.
If we create a circle with a radius I ∗ ω ∗ s i n ( 4 5 ∘ ) , then the change in angular momentum of precession is, Δ A n g u l a r M o m e n t u m = I ∗ ω ∗ s i n ( 4 5 ∘ ) ∗ Δ β where beta is the measure of our subtending angle.
Solving for beta yields I ∗ ω ∗ s i n ( 4 5 ∘ ) Δ A n g u l a r M o m e n t u m = Δ β
Since Δ t i m e Δ A n g u l a r M o m e n t u m = t o r q u e ,
I ∗ ω ∗ s i n ( 4 5 ∘ ) ∗ Δ t i m e Δ A n g u l a r M o m e n t u m = Δ t i m e Δ β
I ∗ ω ∗ s i n ( 4 5 ∘ ) ∗ Δ t i m e Δ A n g u l a r M o m e n t u m = ω p r e c e s s i o n
I ∗ ω ∗ s i n ( 4 5 ∘ ) t o r q u e = ω p r e c e s s i o n
I ∗ ω ∗ s i n ( 4 5 ∘ ) m ∗ g ∗ l ∗ s i n ( 4 5 ∘ ) = ω p r e c e s s i o n
* I ∗ ω m ∗ g ∗ l = ω p r e c e s s i o n *
Since the center of mass of the top is experiencing circular motion, there must be a centripetal force being provided by friction.
Using the formula for centripetal force,
m ∗ r ∗ ω p r e c e s s i o n 2 = F f r i c t i o n
where r is the distance from the center of mass to the point of rotation. Since we are viewing this on a 2-D plane, the "radius" is l ∗ s i n ( 4 5 ∘ )
Plugging in numbers,
0 . 5 ∗ 0 . 1 ∗ s i n ( 4 5 ∘ ) ∗ ( 0 . 0 0 2 ∗ 3 5 0 0 . 5 ∗ 9 . 8 ∗ 0 . 1 ) 2 = 0 . 0 1 7 3 N
Additional Notes
- I = 2 g ⋅ m 2 is not a formula! It is giving you the moment of inertia in g r a m s ⋅ m e t e r s 2 . One has to convert it to k i l o g r a m s ⋅ m e t e r s 2 for this problem.
- If you still have trouble understanding the derivation of the angular velocity of precession, the following picture should help.
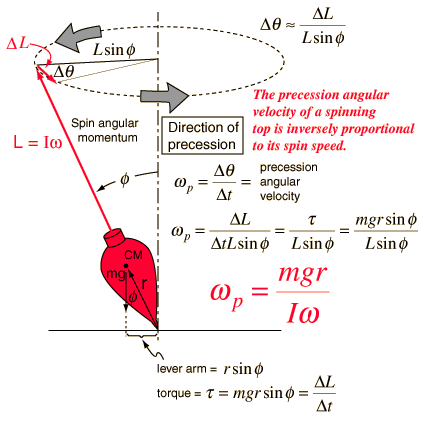 Top
Top
Source: http://hyperphysics.phy-astr.gsu.edu/hbase/mechanics/imgmech/toppre.gif
Very nice expression of spin angular momentum :D. Although I don't understand much words in English, but I can easily understand through your image
Thanks! :)
Thanks for the solution
A spinning top like this will precess due to the torque exerted by its weight. It can be shown that the angular speed of precession ω p is given by
ω p = I ω m g l
Because the top precesses, the center of mass (COM) moves in a circle of radius r = l sin θ . Friction must be the force responsible for keeping the COM moving in a circle since the normal and gravitational forces have no components in the direction of the radius of the circle. Therefore the frictional force is given by
F = m ω p 2 r = m ω p 2 l sin θ = m ( I ω m g l ) 2 l sin θ
After plugging values in to the above equation we arrive at
F = 0 . 0 1 7 3 N
The net torque acting on an object is the time derivative of its angular momentum about its axis of rotation τ = d L / d t (1)
With respect to the tip of the top O, τ O = m g l s i n φ (2)
where m is the mass of the top, l is the distance from O to the center of mass of the top and φ is the angle of inclination of the axis of rotation of the top with respect to the z axis.
Since the top is inclined, it will undergo precession. Observing the above the z axis,
d L / L s i n φ = t a n ( d φ ) = d φ (3)
where L is the angular momentum of the top at its axis of rotation, L s i n φ is the component of the angular momentum on the xy plane, d L is the change in angular momentum as it undergoes precession and d φ is the angular displacement of the axis of rotaion on the xy plane.
Therefore, d L = L s i n φ t a n ( d φ ) = L s i n φ d φ (4)
Using (1) (2) and (4),
d L / d t = L s i n φ d φ / d t = m g l s i n φ (5)
d φ / d t = m g l / L (6)
where d φ / d t is the angular speed of precession of the axis of rotation along the xy plane.
Also, L = I ω (7)
To find the frictional force f ,
f = m ( d φ / d t ) 2 l s i n φ (8)
errata: in equation (3), d L / L s i n φ = t a n ( d θ ) = d θ L s i n φ t a n ( d φ ) = L s i n φ d θ (4) d L / d t = L s i n φ d θ / d t = m g l s i n φ (5) d θ / d t = m g l / L (6) f = m ( d θ / d t ) 2 l s i n φ (8)
To solve this problem, we first note that there is a torque induced on the spinning top due to gravity. We can write this as τ = l × F g . However, the spinning top does not simply fall down because of torque-induced precession. The spinning top will start rotating around the axis that is normal to the horizontal, which we will denote as Ω . By definition, Ω = d t d θ , and we can write d θ = L s i n ϕ d L , where L is the angular momentum, and ϕ is the 4 5 ∘ angle. The infinitesimal change in the angle is a result of the changing angular momentum caused by the torque (a picture can be drawn to confirm this). Thus we can rewrite the expression as Ω = L s i n ϕ 1 d t d L , but note that L = I ω , where I is the moment of inertia of the top spinning about its own axis, and ω is the angular velocity around its own axis. The torque is also written as τ = d t d L , so subbing everything in gives Ω = I ω m g l . Now that we have the angular velocity about the centre axis, note that there is a centripetal force acting on the centre of mass. In order for the tip of the top to stay in one spot, this is also equal to the force of friction (else it will slide around). This can be written as f = m Ω 2 l s i n ϕ . Subbing in for Ω , we get the final equation for the force of friction: f = 2 1 I 2 ω 2 m 3 g 2 l 3 = 0 . 0 1 7 3 N .