Dark shadow
In a Cartesian coordinate system, there are 2 spheres and 1 plane described as follows:
- S 1 : Centered at the origin with radius 1.
- S 2 : Centered at ( 1 0 , 2 , 1 ) with radius 3.
- P : Defined by the equation 9 x − 1 0 z = 2 6 0 .
The first sphere S 1 acts as a light source, the second sphere S 2 is opaque, and the plane P is a screen.
What is the area of the umbra (the darkest part of the shadow, where an observer cannot see the light source at all) on the screen?
The answer is 357.59280144.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
That's fantastic!
Great and hard jop.
There are some mistakes. 4th paragraf, it's 1/OB instead of 1/sqrt(105). 9th paragraf it's <BOA=arcsin(2/sqrt(105)). The same on the 10th paragraph and at the next line it's <OFG-<GFI instead of <OFG-<OFI. I think that's all but I didn't revise number by number ;).
Thanks again.
Log in to reply
You are correct on all cases, and I edited my solution. Thanks so much for your attention to detail!
The shadow is the elliptical intersection of the cone defined by the two spheres and the given plane.
This problem has been addressed here . In the solution of that problem, it is shown that the major and minor semi-axes of the ellipse of intersection are given by:
a = 1 − sin 2 ϕ sec 2 θ z 0 tan θ cos ϕ
b = 1 − sin 2 ϕ sec 2 θ z 0 tan θ cos ϕ
To apply these formulas, we need to calculate z 0 , θ and ϕ , where z 0 is the distance along the axis of the cone between the apex and the
intersection of the cone axis with the cutting plane, and θ is the semi-vertical angle of the cone, and ϕ is the angle between
the axis of the cone and the normal to the cutting plane.
First, we notice that the semi-vertical angle is given by θ = sin − 1 1 0 2 + 2 2 + 1 2 3 − 1 = sin − 1 1 0 5 2
Next, the distance between the apex and the center of S 1 is simply d = sin θ 1 = 2 1 1 0 5
The unit vector along the axis of the cone is u = 1 0 5 1 ( 1 0 , 2 , 1 )
Therefore the apex is located at
( 0 , 0 , 0 ) − d u = ( 0 , 0 , 0 ) − 2 1 ( 1 0 , 2 , 1 ) = ( − 5 , − 1 , − 2 1 )
Now we find the intersection of the cone axis with the cutting plane. The parametric equation of the axis is thus
p = ( − 5 , − 1 , − 2 1 ) + t u
Since u is a unit vector then t represents the distance from the apex ( − 5 , − 1 , − 2 1 ) .
Substituting the point p into the equation of the plane, results in,
9 ( − 5 + 1 0 5 1 0 t ) − 1 0 ( − 2 1 + 1 0 5 1 t ) = 2 6 0
From which z 0 = t = 8 3 0 1 0 5
Finally, we need to find ϕ the angle between the axis of the cone and the normal to the cutting plane.
ϕ = cos − 1 9 2 + 1 0 2 1 0 5 ( 9 , 0 , − 1 0 ) ⋅ ( 1 0 , 2 , 1 ) = cos − 1 1 8 1 1 0 5 8 0
We're done. We now just substitute the values of z 0 , θ and ϕ into the formulas to get the lengths of the semi-major and semi-minor axes.
This gives us,
a = 1 4 . 2 9 2 5 2 0 9 6 and b = 7 . 9 6 3 9 7 8 0 9 8 , resulting in an ellipse area of
Area = π a b = 3 5 7 . 5 9 3
If we consider a cone of semi-vertical angle α intersected by a plane P whose normal makes an angle β with the axis of the cone, then U ( cos ( α − β ) O X cos α , cos ( α − β ) O X sin α ) V ( cos ( α + β ) O X cos α , − cos ( α + β ) O X sin α ) (using a coordinate system with O as origin, with the positive x -axis along the axis of the cone, and with the normal to the plane P being perpendicular to k ) and hence O U = cos ( α − β ) O X O V = cos ( α + β ) O X U V = cos ( α − β ) cos ( α + β ) O X sin 2 α
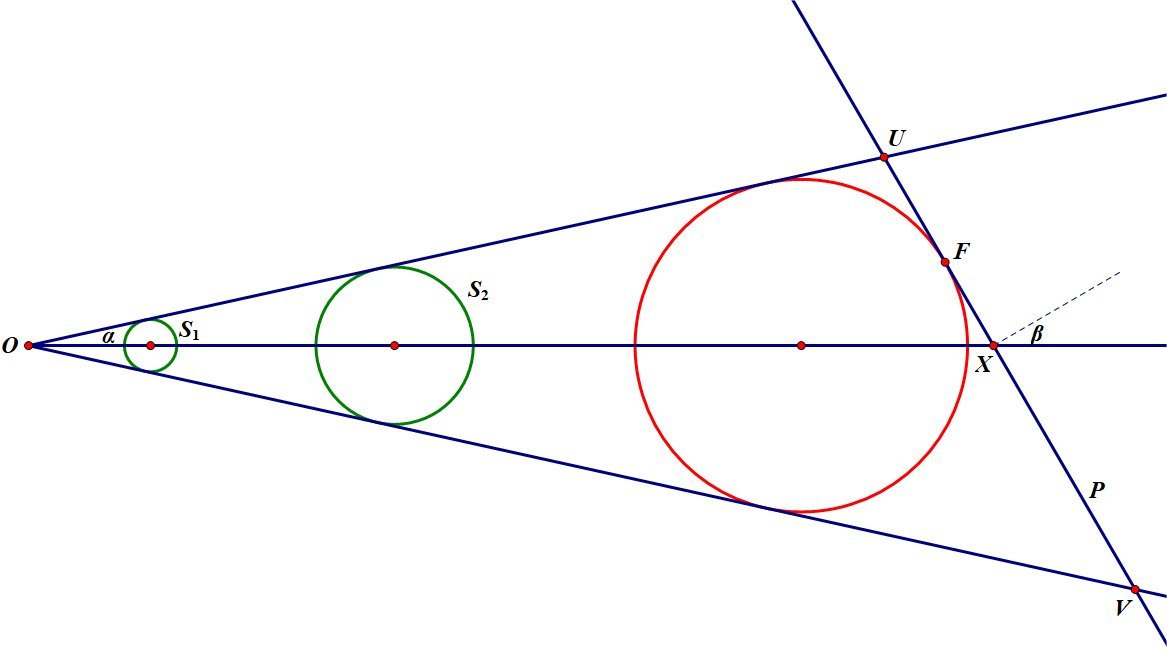
The cone intersects with the plane in an ellipse provided that α + β < 2 1 π . Then U V will be the major axis of the ellipse, and the point of intersection F of the sphere that is inscribed inside the cone and is tangential to the plane P (show in the diagram as the incircle to the triangle O U V ) will be one of the foci of the ellipse. If the ellipse has semi-major axis A and eccentricity E , this means that its area is π A 2 1 − E 2 and that 2 A A ( 1 − E ) = U V = cos ( α − β ) cos ( α + β ) O X sin 2 α = U F = s − O V = cos ( α − β ) cos ( α + β ) O X sin α ( cos α − sin β ) where s is the semiperimeter of the triangle O U V , and hence E = cos α sin β In this case, we are interested in the cone that is tangent to both spheres, which has its vertex O at (in the original coordinate system) ( − 5 , − 1 , − 2 1 ) . The vector u = ⎝ ⎛ 1 0 2 1 ⎠ ⎞ points along the cone's axis. Since the radius of the two spheres differ by 2 , while their centres are a distance 1 0 5 apart, we see that the semi-vertical angle α of the cone is α = sin − 1 1 0 5 2 The point X has coordinates ( 1 0 λ , 2 λ , λ ) where 9 0 λ − 1 0 λ = 2 6 0 , so that λ = 4 1 3 . Thus O X = ( λ + 2 1 ) 1 0 5 = 4 1 5 1 0 5 Finally n = ⎝ ⎛ 9 0 − 1 0 ⎠ ⎞ is normal to the plane P . Considering the scalar product u ⋅ n = 8 0 , we deduce that β = cos − 1 1 8 1 × 1 0 5 8 0 Thus we calculate the desired area to be π A 2 1 − E = 4 7 3 5 0 0 0 4 7 3 5 4 8 4 3 π = 3 5 7 . 5 9 3
nice solution sir
Let O be the apex of the cone whose curved sides are tangent to the spheres S 1 and S 2 . Then the umbra will be the intersection of this cone and plane P which by definition of a conic section will be an ellipse. Let F be the intersection of the cone's axis and plane P , and let plane Q be the plane perpendicular to the cone's axis through point F . Then an umbra on plane Q , also by definition of a conic section, would be a circle.
Since the cone and spheres have rotational symmetry around the cone's axis, we can rotate the whole system so that the line of intersection between planes P and Q is orthogonal to the picture below (so it appears as a point at F ).
Then in this rotational cross-section, let B be the center of sphere S 1 , D be the center of sphere S 2 , A be the point of tangency between O and sphere S 1 , B be the point of tangency between O and sphere S 2 , E be the intersection of O A and plane Q , G be the intersection of the other tangent line and plane Q , H be the intersection of O A and plane P , and I be the intersection of the other tangent line and plane P .
△ O A B and △ O C D are similar by angle-angle similarity, so O B A B = O D C D . A B is the radius of sphere S 1 so A B = 1 , and C D is the radius of sphere S 2 so C D = 3 . Since B is ( 0 , 0 , 0 ) and D is ( 1 0 , 2 , 1 ) , B D = 1 0 5 by the distance formula. Finally, since O D = O B + B D , O D = O B + 1 0 5 . Therefore, the ratio becomes O B 1 = O B + 1 0 5 3 , and solving this gives O B = 2 1 0 5 .
Since O B is half of B D , and B is at the origin, the coordinates of O are the negative half of the coordinates of D , so O is − 2 1 ( 1 0 , 2 , 1 ) = ( − 5 , − 1 , − 2 1 ) .
F is on the vector B D , which can be defined by the vector equation ( x , y , z ) = ( 1 0 t , 2 t , t ) . F is also on plane P , which has an equation of 9 x − 1 0 z = 2 6 0 . Therefore, at F , 9 ( 1 0 t ) − 1 0 ( t ) = 2 6 0 , so t = 4 1 3 , and its coordinates are ( 1 0 ( 4 1 3 ) , 2 ( 4 1 3 ) , 4 1 3 ) = ( 2 6 5 , 2 1 3 , 4 1 3 ) .
Since O is ( − 5 , − 1 , − 2 1 ) and F is ( 2 6 5 , 2 1 3 , 4 1 3 ) , O F = 4 1 5 1 0 5 by the distance formula.
△ O A B and △ O F E are similar by angle-angle similarity, so A B O A = E F O F . Since A B = 1 and O B = 2 1 0 5 (from above), then by Pythagorean's Theorem on △ O A B , O A = 2 1 0 1 , and since O F = 4 1 5 1 0 5 , the ratio becomes 1 2 1 0 1 = E F 4 1 5 1 0 5 , and solving this gives E F = 2 0 2 1 5 1 0 6 0 5 . Therefore, a circle projected from the cone onto plane Q would have a radius of 2 0 2 1 5 1 0 6 0 5 .
∠ E F H is the angle between plane P and plane Q , which is the same measurement of the angle between a vector perpendicular to plane P and a vector perpendicular to plane Q . A vector perpendicular to plane Q is vector B D = ( 1 0 , 2 , 1 ) , and since the equation of plane P is 9 x − 1 0 z = 2 6 0 , a vector perpendicular to it is ( 9 , 0 , − 1 0 ) . The angle between these two vectors can be found by solving cos θ = ∣ ( 9 , 0 , − 1 0 ) ∣ ∣ ( 1 0 , 2 , 1 ∣ ( 9 , 0 , − 1 0 ) ∙ ( 1 0 , 2 , 1 ) , and so ∠ E F H = θ = cos − 1 ( 3 8 0 1 1 6 1 9 0 0 5 ) .
Looking at △ O F H , we have ∠ F O H = ∠ O A B = sin − 1 ( 1 0 5 2 1 0 5 ) from △ O A B , O F = 4 1 5 1 0 5 , and ∠ O F H = ∠ O F E + ∠ E F H = 2 π + cos − 1 ( 3 8 0 1 1 6 1 9 0 0 5 ) . Then using the law of sines we can determine that F H = 1 8 9 2 2 0 0 1 8 2 8 1 + 5 2 2 8 1 5 0 5 .
Similarly, looking at △ O F I , we have ∠ F O I = ∠ O A B = sin − 1 ( 1 0 5 2 1 0 5 ) from △ O A B , O F = 4 1 5 1 0 5 , and ∠ O F I = ∠ O F G − ∠ G F I = 2 π − cos − 1 ( 3 8 0 1 1 6 1 9 0 0 5 ) . Then using the law of sines we can determine that F I = 1 8 9 2 2 0 0 1 8 2 8 1 − 5 2 2 8 1 5 0 5 .
Now here is a picture of this ellipse projected onto plane P , where the points F , H , and I are now represented as vertical lines, and the ellipse's center is redefined at the origin.
The horizontal length of the ellipse is I F + F H , so its major axis a is a = 2 1 ( I F + F H ) = 2 1 ( 1 8 9 2 2 0 0 1 8 2 8 1 − 5 2 2 8 1 5 0 5 + 1 8 9 2 2 0 0 1 8 2 8 1 + 5 2 2 8 1 5 0 5 ) = 4 7 3 5 0 1 8 2 8 1 .
Since we know that the projection of the cone on plane Q is a circle with a radius of r = 2 0 2 1 5 1 0 6 0 5 , and F is on plane P and plane Q , the ellipse's height at x = F is also r . The x -value of F is x = 2 1 ( I F + F H ) − I F = 2 1 ( 1 8 9 2 2 0 0 1 8 2 8 1 − 5 2 2 8 1 5 0 5 + 1 8 9 2 2 0 0 1 8 2 8 1 + 5 2 2 8 1 5 0 5 ) − 1 8 9 2 2 0 0 1 8 2 8 1 − 5 2 2 8 1 5 0 5 = 1 8 9 2 5 2 2 8 1 5 0 5 and so the ellipse passes through the coordinate ( 1 8 9 2 5 2 2 8 1 5 0 5 , 2 0 2 1 5 1 0 6 0 5 ) . Using the standard horizontal ellipse formula a 2 x 2 + b 2 y 2 = 1 , the above a value, and the above coordinate as x and y values, we can find that the minor axis b is b = 4 7 3 1 0 0 1 4 1 9 .
Finally, the area of an ellipse is A = π a b = π ⋅ 4 7 3 5 0 1 8 2 8 1 ⋅ 4 7 3 1 0 0 1 4 1 9 = 2 2 3 7 2 9 5 0 0 0 π 2 5 9 4 0 7 3 9 ≈ 3 5 7 . 5 9 2 8 0 1 4 4 .