Dart board problems
On the dart board shown in the figure below, the outer circle has radius 6 and the inner circle has radius 3.
Three radii divide each circle into three congruent regions, with point values shown.
The probability that a dart will hit a given region is proportional to the area of the region.
After two darts hit this board, the final score is the sum of the point values in the regions.
If the probability that the final score, after you hit the board with two darts, is odd is a/b,
where a,b are positive coprime integers, then what is a + b ?
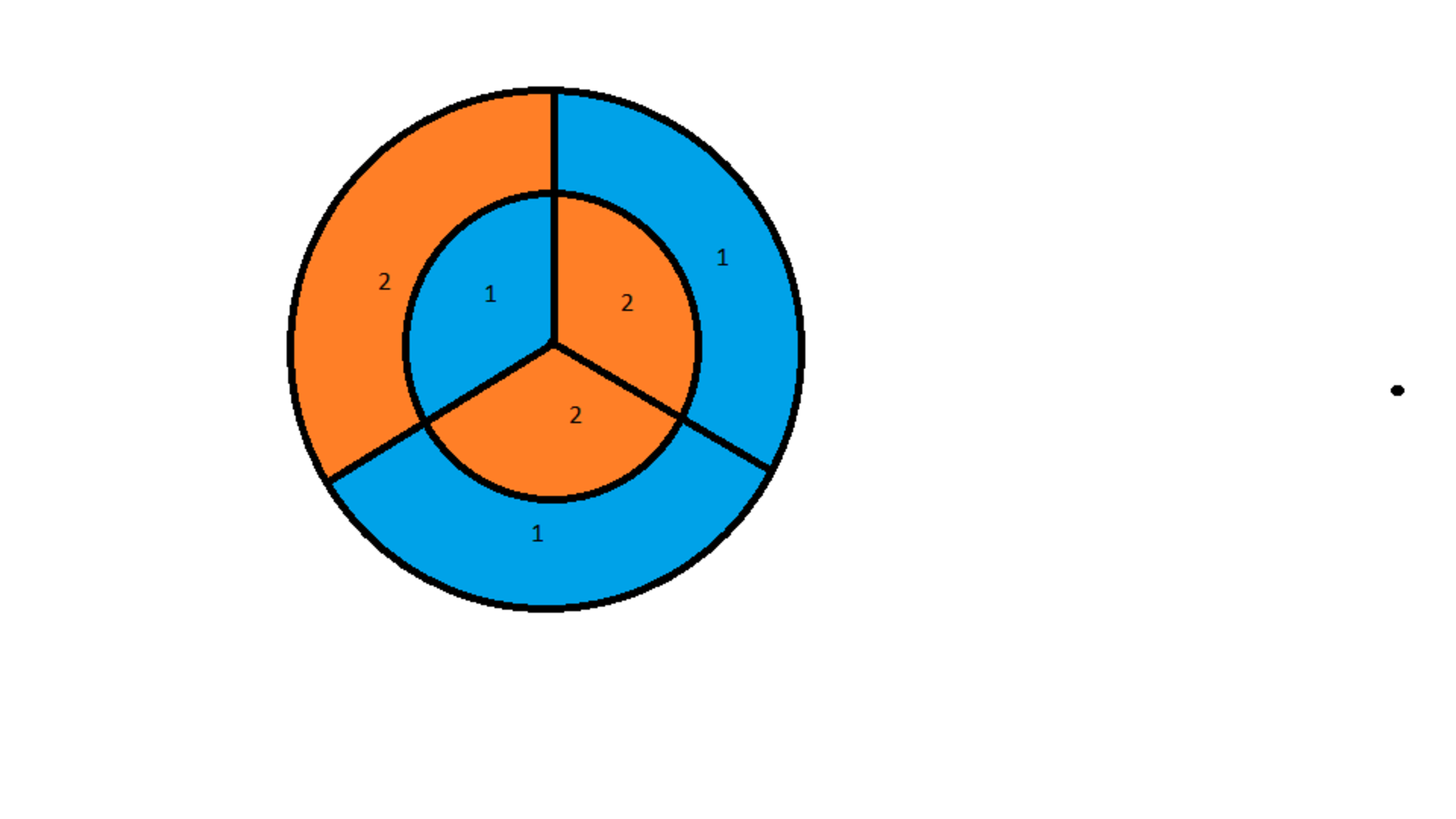
The answer is 107.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since there are only 1-point- and 2-point-fields on the board, ths only way to get an odd sum is to have 3 points, so either 1 and then 2 or 2 and then 1.
The area of the dartboard is given by A b o a r d = π r 2 = 3 6 π . To get the area of the orange regions (for 2 points), we imagine rotating the inner circle by 120° so that the big and a small orange region line up to have area A o r a n g e 1 = 3 1 A b o a r d = 1 2 π . The other orange region is one third of the smaller circle with radius 3, so it has an area of A o r a n g e 2 = 3 1 π r 2 = 3 π . In total, the orange regions have an area of A o r a n g e = A o r a n g e 1 + A o r a n g e 2 = 1 2 π + 3 π = 1 5 π .
The area of the blue regions is just A b l u e = A b o a r d − A o r a n g e = 3 6 π − 1 5 π = 2 1 π .
The probability of an odd sum is p ( 1 ) ⋅ p ( 2 ) + p ( 2 ) ⋅ p ( 1 ) = 2 p ( 1 ) p ( 2 ) . p ( 1 ) = 3 6 π 2 1 π = 1 2 7 , p ( 2 ) = 3 6 π 1 5 π = 1 2 5 .
2 p ( 1 ) p ( 2 ) = 2 ⋅ 1 2 7 ⋅ 1 2 5 = 7 2 3 5 .
Therefore, a + b = 3 5 + 7 2 = 1 0 7 .