Dart plane
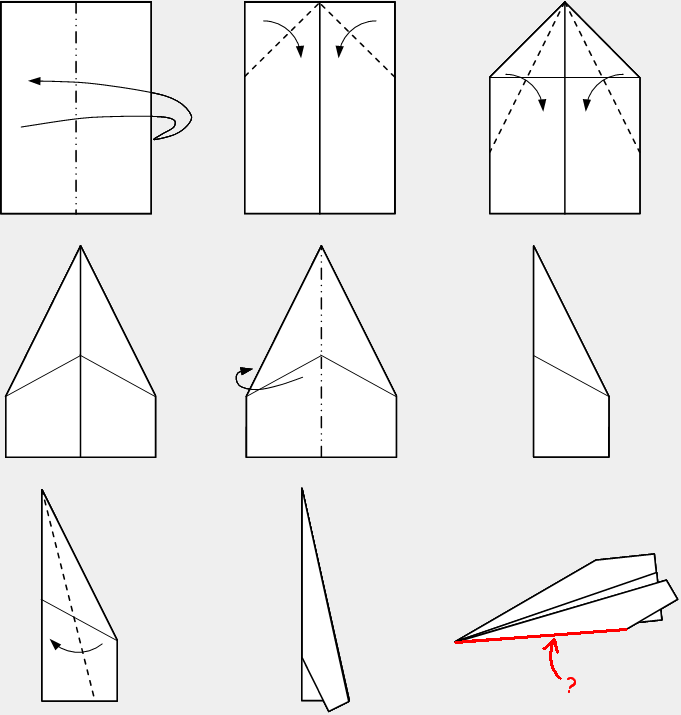 This is how to make a traditional paper plane using an A4 paper (
mm). What is the length of the side in red (in mm)?
This is how to make a traditional paper plane using an A4 paper (
mm). What is the length of the side in red (in mm)?
Round your answer to the nearest hundredth.
The answer is 274.38.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
It is first helpful to understand the axioms of paper folding, which were derived by Humiaki Huzita and Koshiro Hatori, both mathematicians and origami artist. Thus, the name of these axioms is Huzita-Hatori axioms . The latest known axiom was then discovered by Robert J. Lang who is the greatest origami artist for creating complex designs.
I suggest you to take the time to read them as there are applications of folding to real life situations!
Here is the paper plane unfolded:
In the given illustration, in Step 7 (bottom-left), since the long slanted line is unaffected by the fold, we determine its length, considering the following diagram and first few steps:
Without loss of generality, since the steps show the same type of folds for both sides of the rectangles, we can assume that the origami is symmetric. Therefore, ∣ E I ∣ = ∣ G E ∣ .
In Step 1 , folding the paper in half forms the midpoint of the shortest side length of the A4 paper, which shows that ∣ A E ∣ = ∣ E B ∣ = 1 0 5 .
In Step 2 , folding diagonally toward the crease bisects the right angles of both thinnest rectangles. In this case, ∠ A E I = ∠ E I H = ∠ H E F = ∠ F E B = 4 5 ∘ . With the help of 4 5 - 4 5 - 9 0 triangle ratio, ∣ J E ∣ = ∣ F E ∣ = 1 0 5 2 .
In Step 3 , two flaps are both folded toward the vertical lines. By Axiom 2 , J H is perpendicular to E I . Likewise, E G ⊥ H F . Then, since the fold bisects the angle of 4 5 ∘ , Δ E J H and Δ E H F are both isosceles of side length 1 0 5 2 and base angles 6 7 . 5 ∘ . However, Δ H I J and Δ F G H are also isosceles of the same angles and sides since the fold depends on the folding point H .
Thereby, E H I J and E F G H are both rhombuses of length 1 0 5 2 and angles 4 5 ∘ and 1 3 5 ∘ . Thus, by Cosine Rule , the length of the red line is ∣ G E ∣ = ∣ E I ∣ = 1 0 5 2 2 − 2 cos ( 1 3 5 ∘ ) = 1 0 5 4 + 2 2 ≈ 2 7 4 . 3 8
Note: It is also possible to show this by focusing on finding the length of A I or B G . Then, apply the Pythagorean Theorem .