Dartboard Probability
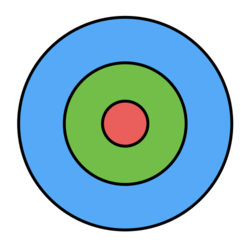 The dartboard above is made up of three concentric circles with radii
1
,
3
,
and
5
.
Assuming that a dart thrown will land randomly on the dartboard, what is the probability that it lands in the green region?
The dartboard above is made up of three concentric circles with radii
1
,
3
,
and
5
.
Assuming that a dart thrown will land randomly on the dartboard, what is the probability that it lands in the green region?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
With the potential for paddling, I believe the possibilities must be carefully estimated further, because sound scare, water upset, etc. must be included. I don't think simple mathematics is all that is needed.
32% .The areas of the three circles are 1, 9 and 25 pie squares. The area where the dart can hit will be 1,8,16 pie squares. For the dart to hit the green area the probability will be 8/25 ie 32%.
Says I am incorrect and I had the same reasoning
The area of the red, green and blue shaded regions are π,8π,16π, So probability that the dart will hit the green region is =8π/(π+8π+16π) Which is equal to 8/25or 32%
The explanations that people have given, i think, are not correct. If the "circles" are of radii 1, 3, and 5, then the regions will have the areas - π, 3π and 5π respectively (using ring formula where the area of the ring = π ( R 2 - r 2 ) The answer will be the same, but explanation different.
I was thinking with that in mind but slightly different, π(r^2)(2/5) = 25π (2/5) = 10π or 40% where did I go wrong?
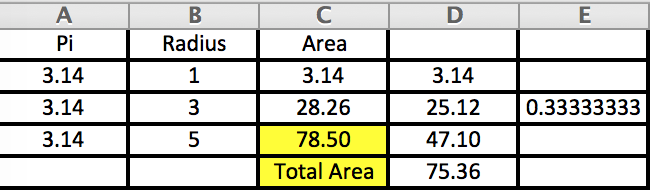
My answer is far less accurate and probably involves some luck. I figured out the area of each circle and then subtracted the area of the inner circle as shown in Column D. I then divided that number (25.12) by the sum of Column D (75.36) = .3333 which was closer to 32% than it was to 36%.
Moderator note:
That is the correct approach. The reason why your answer is off slightly, is because you used approximate values to find n π , instead of just leaving it in terms of π .
All 3 regions together is 100%. That is an area of 25 pi. So, each pi represents an area of 4. The ring in the middle has an area of 8 pi. And, 8 x 4 = 32%.
The easiest way is to factor out π after calculating the areas of the circles (since they all involve it) and just deal with the coefficients:
r = 1 g = 8 (i.e., 9 - r) b = 16 (i.e., 15 - g - r)
Thus, ratio of g to entire set of circles is 8/(16+8+1) = 0.32.
The area of the green circle, ignoring the red circle, is 3 2 π = 9 π . The area of the red circle is 1 2 π = π . Thus, the area of the green region is 9 π − π = 8 π .
The area of the entire dartboard is 5 2 π = 2 5 π , so the probability that it is in the green region is 2 5 π 8 π = 3 2 % .