Daughter Triangles
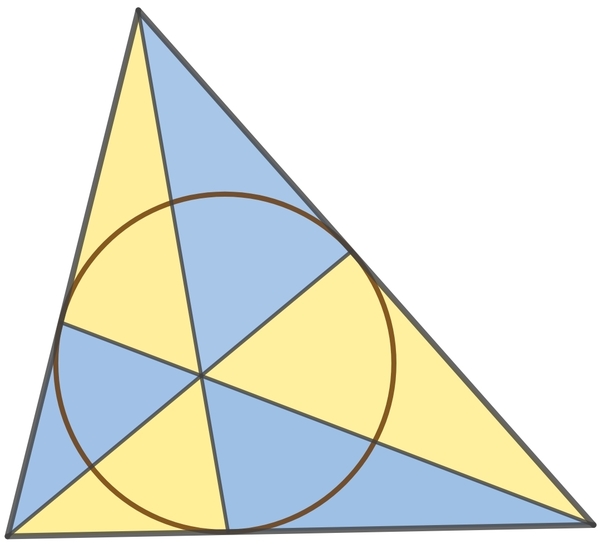 Consider a triangle in which we draw line segments connecting the vertices of the triangle to the points of tangency of the incircle on the opposite sides. This divides the original triangle into six 'daughter' triangles.
Consider a triangle in which we draw line segments connecting the vertices of the triangle to the points of tangency of the incircle on the opposite sides. This divides the original triangle into six 'daughter' triangles.
If one of these daughter triangles is an equilateral triangle, then find the ratio of the area of the original triangle to that of the equilateral daughter triangle.
The answer is 33.6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The three cevians through the points T A , T B , T C of tangency with the incircle are concurrent at the Gergonne point G e . Suppose that A T C G e is equilateral. We know that A T A 2 = c 2 + ( s − b ) 2 − 2 ( s − b ) c cos B C T C 2 = a 2 + ( s − b ) 2 − 2 ( s − b ) a cos B cos B = 2 a c a 2 + c 2 − b 2
at all times. Since the angles ∠ T A A B = ∠ A T C C = 6 0 ∘ , we also deduce that ( s − b ) 2 = A T A 2 + c 2 − c A T A b 2 = ( s − a ) 2 + C T C 2 − ( s − a ) C T C These equations are all homogeneous of degree 2 , and so we can attempt to solve for b , c in terms of a . It turns out that there are only two real solutions of these equations:
The first solution only produces a trivial triangle, so the second is the only proper solution. If we put a = 4 9 , b = 1 9 and c = 4 0 , then s = 5 4 . Thus the equilateral triangle A T C G e has area 4 3 ( s − a ) 2 = 4 2 5 3 . On the other hand the original triangle has area s ( s − a ) ( s − b ) ( s − c ) = 2 1 0 3 , and hence the ratio of areas is 2 5 3 2 1 0 3 × 4 = 5 1 6 8 = 3 3 . 6