Day 18: An Incredible Result
A triangle A B C has a right angle at B . A semicircle is inscribed within on the side B C and its diameter is equal to A B .
If the ratio B C A B can be written in the form b a where a and b are positive coprime integers, find a + b .
This problem is part of the set Advent Calendar 2014 .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Discussions for this problem are now closed
I found out a solution but since I mixed up the radius with the diameter, I got it wrong, so I shall post my answer here...
I used geometry, which states that the radius of the incircle of a triangle is the area over the semi-perimeter.
I drew a mirror image of the triangle, and put it together, completing the semi-circle. Without loss of generality, I let A B = 2 , and B C = x .
The area of the triangle is now ( 2 + 2 ) ∗ x / 2 = 2 x
The semi-perimeter is ( 4 + 2 x 2 + 4 ) / 2 = 2 + x 2 + 4
The radius of the incircle is: 2 + x 2 + 4 2 x = 1
2 x = 2 + x 2 + 4
2 x − 2 = x 2 + 4
4 x 2 − 8 x + 4 = x 2 + 4
3 x 2 − 8 x = 0
x = 0 , 3 8
We take the value x = B C = 3 8 . B C A B = 3 8 2 = 2 ∗ 8 3 = 4 3
3 + 4 = 7
and nice question! Not to hard yet cannot be eye-powered
Yeah, I figured similar triangles would be the shortest and most elegant approach. Nice question.
Where is the wrong? Area of circle/area of triangle (1/2AB)^2(22/7)/(1/2AB.BC) AB/BC=7/11 Where is the wrong
That is very interesting! The main place where you went wrong is that you haven't formed an equation; you have just simplified the expression. Also you have used a circle instead of a semicircle. It would be best not to use 22/7 for pi if you want an exact answer too.
Hope this helps! :)
In principle, I used this method.
 If you can't see the image here, go to https://i.imgur.com/yyJ0BeC
If you can't see the image here, go to https://i.imgur.com/yyJ0BeC
Sorry if the solution is not legible, but this seems easier than LaTeX :P
Let the center of the semicircle be O , where it touches A C at P and its radius be O P = 1 . Also let D C = x
We note that △ A B C and △ O P C are similar. Therefore,
A B A C = O C O P ⇒ A B A B 2 + B C 2 = 1 1 + x
⇒ 2 2 2 + ( 2 + x ) 2 = 1 + x ⇒ 4 + 4 + 4 x + x 2 = 2 ( 1 + x )
⇒ x 2 + 4 x + 8 = 2 2 ( 1 + x ) 2 ⇒ x 2 + 4 x + 8 = 4 x 2 + 8 x + 4
⇒ 3 x 2 + 4 x − 4 = 0 ⇒ ( 3 x − 2 ) ( x + 2 ) = 0 ⇒ x = 3 2 as x > 0 .
Now, B C A B = 2 + x 2 = 2 + 3 2 2 = 4 3
⇒ a = 3 , b = 4 and a + b = 3 + 4 = 7 .
To make things easier to understand, I will refer to the diagram in Michael Ng's answer. If we reflect the semicircle across B D , segment A B would be tangent to the resulting circle. This means that A B = A F since A F is also tangent to the resulting circle. Now A B = A F = B D = a , E D = E F = 2 a , D C = b , and F C = c .
Pythagorean Theorem over triangle ABC gives us: a 2 + ( a + b ) 2 = ( a + c ) 2 which simplifies to: a 2 + 2 a b + b 2 = 2 a c + c 2
Pythagorean Theorem over triangle EFC gives us: ( 2 a ) 2 + c 2 = ( 2 a + b ) 2 which simplifies to: c 2 = a b + b 2
Plug in for c in the first equation and cancel to get: a 2 + a b = 2 a a b + b 2
This cancel a's and square both sides to get: ( a + b ) 2 = 4 ( a + b ) b
Cancel (a+b) and solve for be to get b = 3 a
This means that B C A B = 4 3 so the answer is 7.
It is possible to use trigonometry or calculus but here is an algebraic proof:
As we enlarge the diagram the ratio remains constant so we can assume that A B = 2 without loss of generality. Now name some points as follows: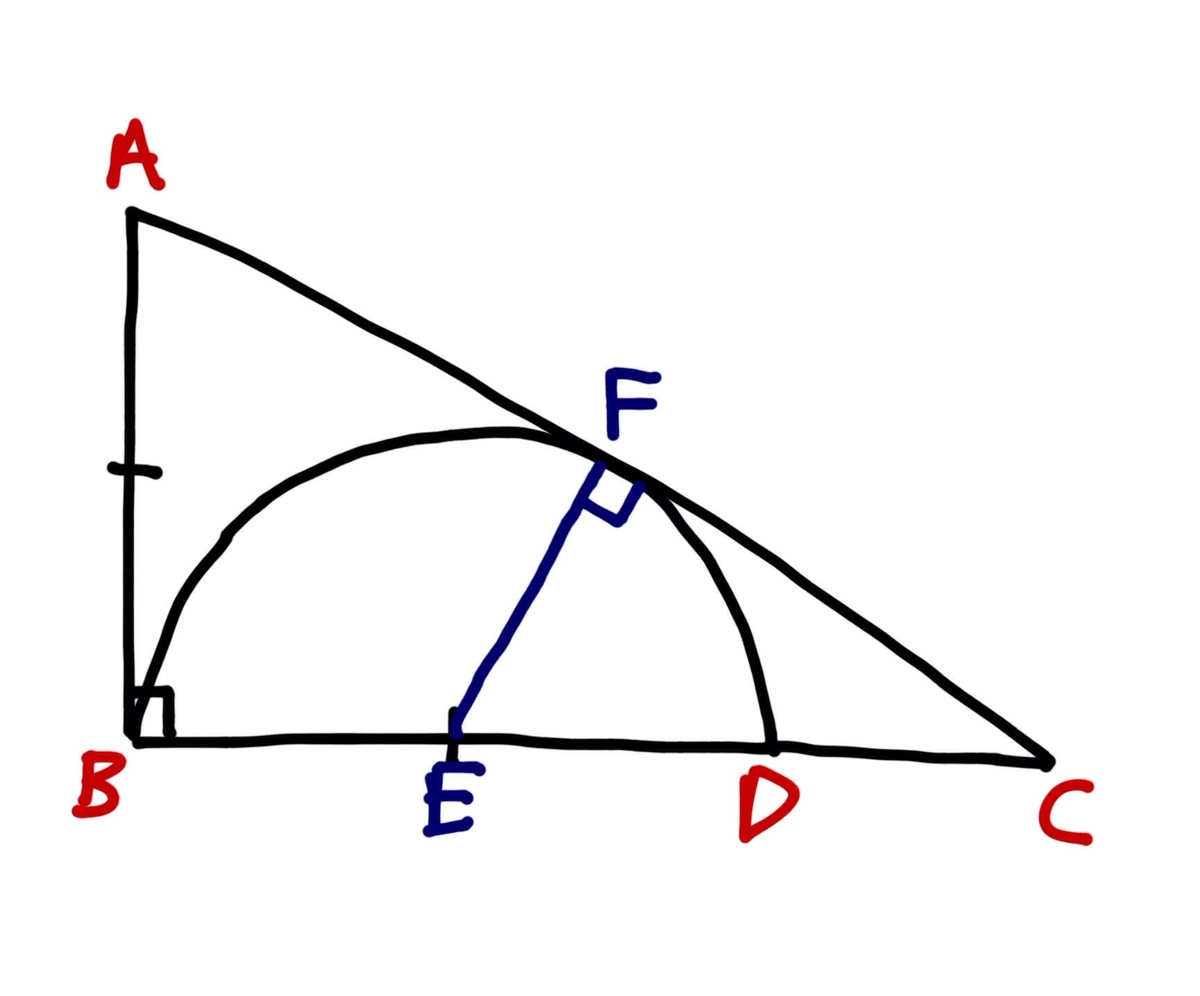
A B C is similar to E F C and E F = 1 . Now let F C = a . Then B C = 2 a and E C = 2 a − 1 . Now by Pythagoras' Theorem on E F C , ( 2 a − 1 ) 2 = a 2 + 1 2 Solving gives a = 3 4 and therefore B C A B = 4 3 which gives the answer 3 + 4 = 7 as required.