Day 21: One and a Half Circles in a Square
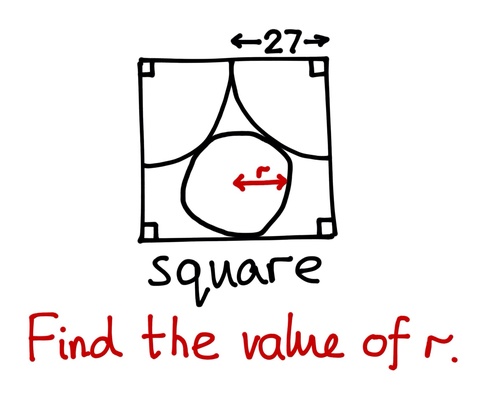 Two quarter circles of radius
2
7
are drawn on adjacent corners of a square. A circle is drawn touching these and the bottom side of the square.
Two quarter circles of radius
2
7
are drawn on adjacent corners of a square. A circle is drawn touching these and the bottom side of the square.
Find the radius of this circle.
This problem is part of the set Advent Calendar 2014 .
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Ah; I didn't see your solution while I was writing mine due to similar timings. Your solution is very clear and I have upvoted it. :)
Log in to reply
Thanks, Michael. Nice problem. A variation you could try is to have the quarter circle on the left have radius 2 4 and the one on the right have radius 3 0 . The question would then be to find the radius of the largest circle that can be inscribed in the remaining portion of the square. As far as I can see this would necessitate the solving of a system of 2 equations, 2 unknowns. The answer is a bit messy but it is possible to get an exact value.
Neat application of Pythagoras' Theorem. Level 3 might be a tad too high?
can you provide a figure with your solution Brian Charlesworth
We first scale the diagram down so that the given radius is
1
for easier calculation, then we will multiply back; it does not affect the result. Now draw in this triangle:
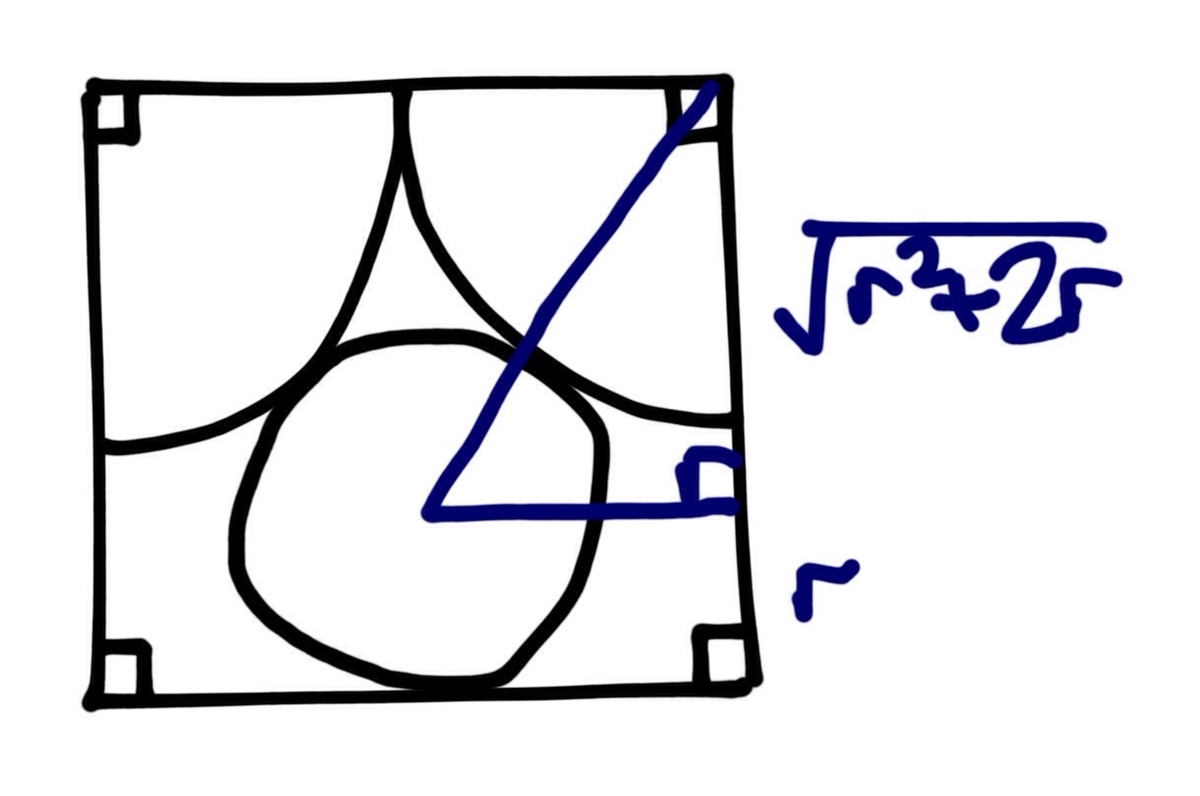 Using Pythagoras' Theorem we can find the height of the square in terms of
r
:
2
=
r
2
+
2
r
+
r
Using Pythagoras' Theorem we can find the height of the square in terms of
r
:
2
=
r
2
+
2
r
+
r
And solving: r 2 − 4 r + 4 = r 2 + 2 r 6 r = 4 r = 3 2
Hence the required answer is 3 2 × 2 7 = 1 8 .
Let the square be A B C D . A and B the two top vertices. Let the midpoints of A B and C D be M and N respectively and the center of the circle be O . Due to symmetry, we find that M O N is a straight line and that:
M N = M O + O N = A O 2 − A M 2 + O N = ( 2 7 + r ) 2 − 2 7 2 + r = 5 4
⇒ ( 2 7 + r ) 2 − 2 7 2 = 5 4 − r
⇒ ( 2 7 + r ) 2 − 2 7 2 = ( 5 4 − r ) 2
⇒ 2 7 2 + 5 4 r + r 2 − 2 7 2 = 5 4 2 − 1 0 8 r + r 2
⇒ 1 6 2 r = 5 4 2 ⇒ r = 1 8
by phythagorth : (27+r)^2=(2r)^2 + (27)*2 in the end of the equation we will get r=18
Suppose that this square is named ABCD such that A and B is the center of the circles having a midpoint of 27. And O is the center of the circle touching these circles and the bottom of the square having a radius of r. Draw a line from the midpoint of AB, M to O and from B to O. From the circle theorem, we have that BMO is a right triangle, so, MB = 27 and BO = 27+r Because MO is a perpendicular on AB and M is the midpoint of AB, MN = AB = 54, where N is the midpoint of CD. So MO = 54-r. By applying the Pythagorean theorem, we have, r = 18.
by phythagorth : (27+r)^2=(2r)^2 + (27)*2 in the end of the equation we will get r=18
Firstly, denote the square as ABCD clockwise from top left to bottom left. Now make the centre of the circle (of radius r) point P and let the midpoint of AB be Q. Draw AP, BP and QP. Now QP is perpendicular to AB (tangent to a radius). Using Pythagoras's Theorem: ( A Q ) 2 + ( Q P ) 2 = ( A P ) 2 . For simplicity, let A Q = Q B = x (27). Now x 2 + ( 2 x − r ) 2 = ( x + r ) 2 . Expanding and rearranging gives r = 3 2 x = 3 5 4 = 18.
Form a triangle with vertex A being the top left corner of the square, vertex B being the center of the radius r circle, and vertex C being the point where the horizontal through B intersects the left side of the square.
Then Δ A B C is a right triangle with hypotenuse A B = 2 7 + r and legs A C = 5 4 − r and B C = 2 7 . Thus, using the Pythagorean Theorem, we have that
( 2 7 + r ) 2 = ( 5 4 − r ) 2 + 2 7 2 ⟹ 5 4 r = 5 4 2 − 1 0 8 r ⟹ r = 1 6 2 5 4 2 = 1 8 .