Day 21: This Diagram Looks Familiar
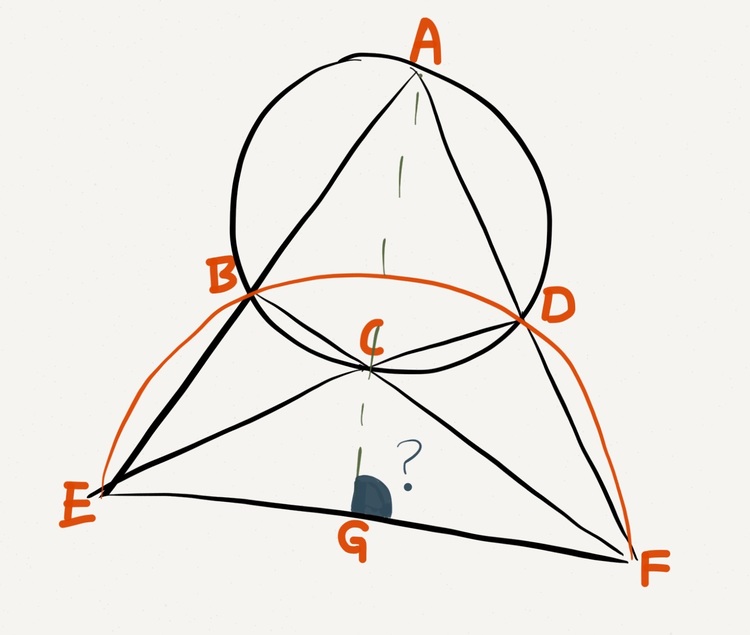 A cyclic quadrilateral
has its sides extended and they do meet, creating points
and
in the diagram.
A cyclic quadrilateral
has its sides extended and they do meet, creating points
and
in the diagram.
As shown, are also concyclic.
Find the angle between line segments and .
This problem is part of the Advent Calendar 2015 .
The answer is 90.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
∠ E B F = ∠ E D F (angles in the same segment)
So ∠ A B C = ∠ A D C . But ∠ A B C + ∠ A D C = 1 8 0 ∘ so both are right angles.
Therefore in triangle A E F , C is the orthocentre; therefore A C is an altitude and so the angle required is 9 0 ∘ as required.