Day 22: A Forest of Lines
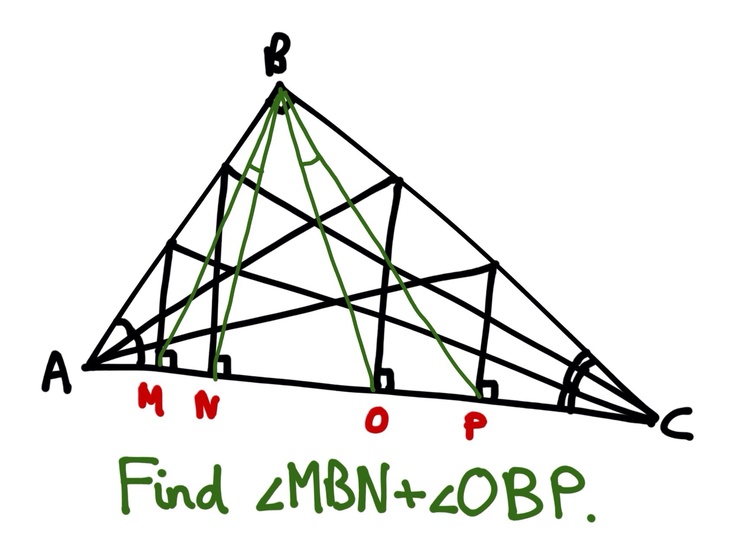 A triangle
is right angled at
. From each of
and
two angle trisectors are drawn to the opposite side, and from each of the four intersections a perpendicular is drawn onto the side
. The feet of these perpendiculars are named
and
in order from
.
A triangle
is right angled at
. From each of
and
two angle trisectors are drawn to the opposite side, and from each of the four intersections a perpendicular is drawn onto the side
. The feet of these perpendiculars are named
and
in order from
.
Find the value of .
This problem is part of the set Advent Calendar 2014 .
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First I shall name the other ends of the trisectors H , G , E and F clockwise from A and call ∠ F A C α and ∠ H C A β :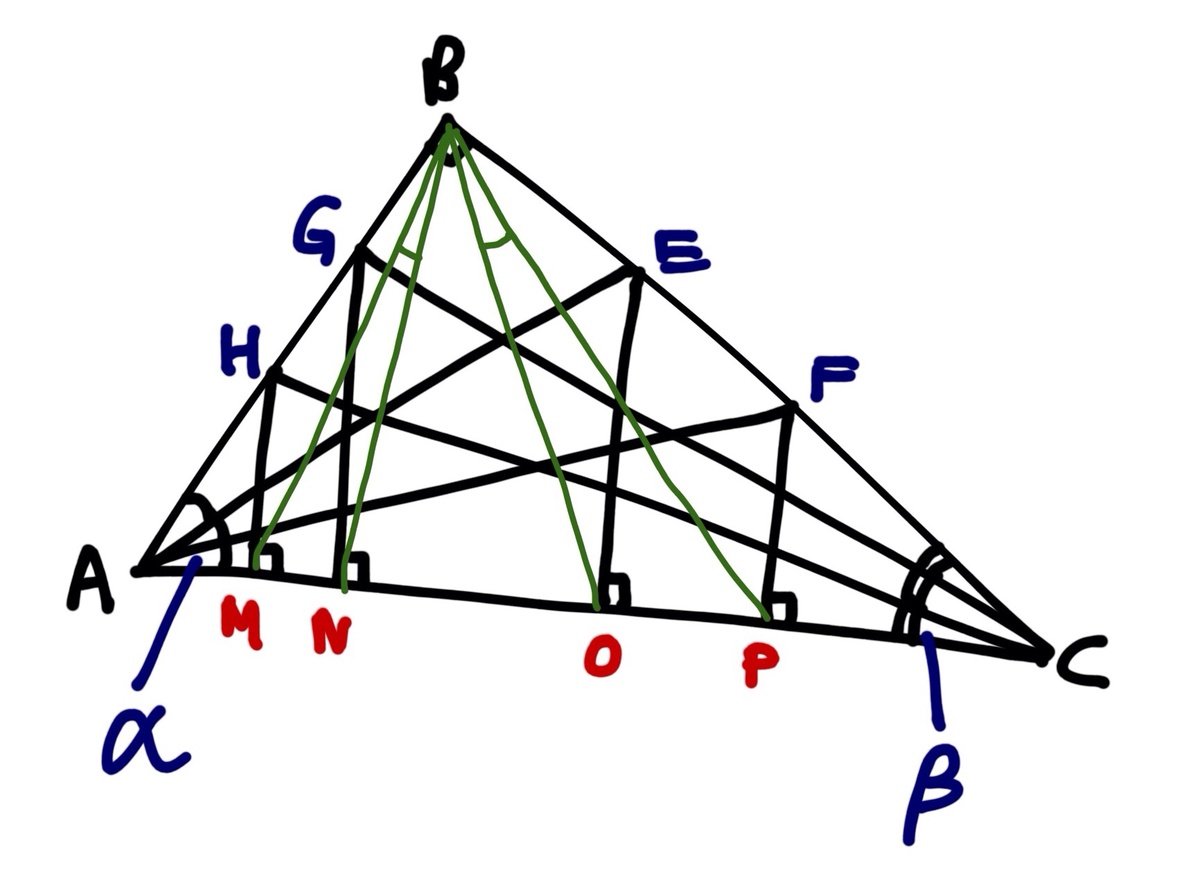
First notice that α + β = 3 0 ∘ due to the angle sum in a triangle.
Now A P F B is cyclic so ∠ P B F = α . We use the same trick to show that ∠ M B H = β . So ∠ M B P = 9 0 ∘ − ( α + β ) = 6 0 ∘ .
We can apply a similar method on cyclic quadrilaterals A O E B and C N G B to show that ∠ N B O = 9 0 ∘ − 2 ( α + β ) = 3 0 ∘ .
Therefore ∠ M B N + ∠ O B P = 6 0 ∘ − 3 0 ∘ = 3 0 ∘