Day 22: Ellipse or Stretched Circle?
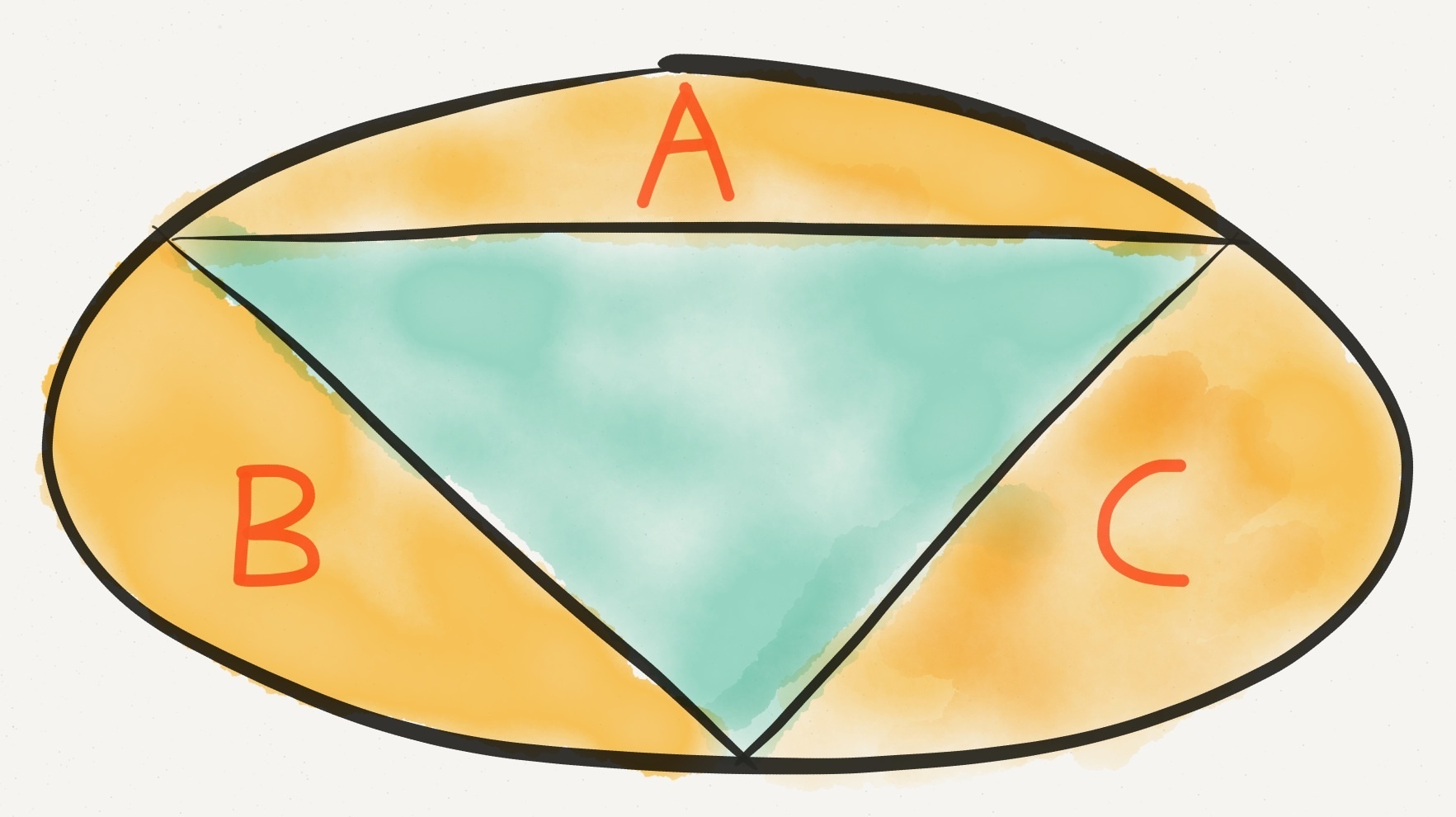
A triangle splits an ellipse into four sections. The three parts that have a curve (shown in the diagram) are of equal area ( ).
Also, the ellipse is three times as long as it is wide, and one side of the triangle is parallel to its major axis.
What is the obtuse angle in the triangle?
This problem is part of the Advent Calendar 2015 .
The answer is 120.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
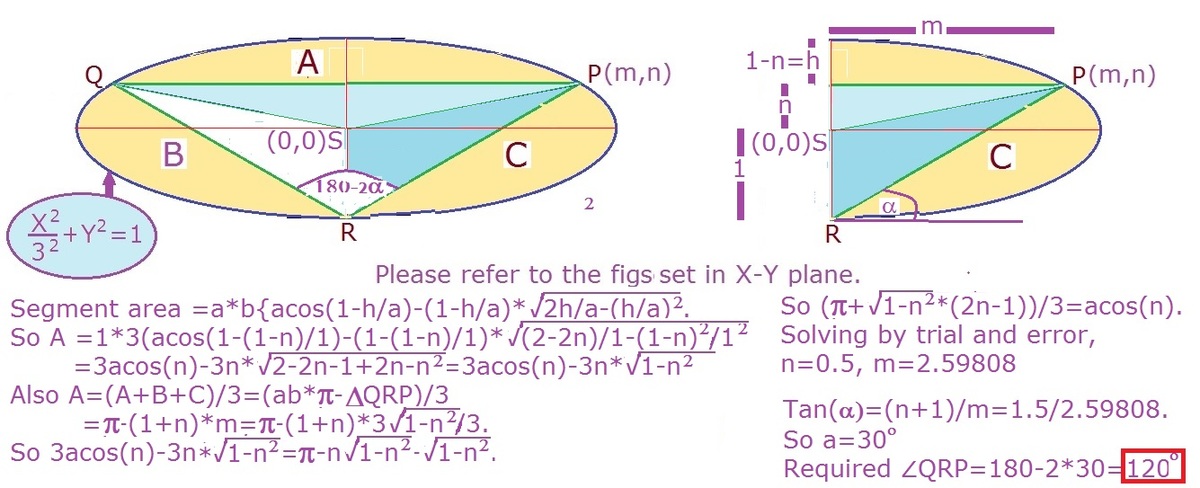
We will use the fact that when you stretch equal areas in the same way, they remain equal. So squeeze the ellipse lengthways to one third of its length, giving a circle.
Now the new A , B , C are still equal so it is clear that the triangle must be equilateral. In an equilateral triangle the height is 2 3 of the sidelength.
Now undo the transformation and stretch the circle back to the ellipse. The side of the triangle parallel to the major axis increases to three times its length, but the height of the triangle remains constant.
So now the triangle's height is 6 3 of its sidelength. The triangle is obviously isosceles so split it into two equal parts. The height is 3 3 of half the sidelength, so we have a 30-60-90 triangle. Therefore the acute angles in the triangle are 3 0 ∘ , and the obtuse angle is 1 2 0 ∘ as required.