Day 3: Inverted Thinking
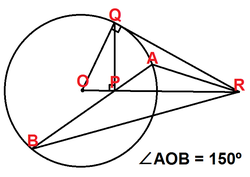 Let
O
be the centre of a circle and let
P
be a point inside this circle. Draw the radius
O
Q
such that
∠
O
P
Q
is a right angle. Let
R
be the intersection of the line
O
P
and of the tangent at
Q
. Let
A
B
be a chord passing through
P
of the circle.
Let
O
be the centre of a circle and let
P
be a point inside this circle. Draw the radius
O
Q
such that
∠
O
P
Q
is a right angle. Let
R
be the intersection of the line
O
P
and of the tangent at
Q
. Let
A
B
be a chord passing through
P
of the circle.
Given that ∠ A O B = 1 5 0 ∘ , find the value of ∠ A R P .
This problem is part of the set Advent Calendar 2014 .
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
A nice result from this is that P R bisects ∠ A R B .
Why is P the inverse of R ?
Log in to reply
That's because ORQ is similar to OQP. Therefore OP.OR = (OQ)^2 by similar triangle ratios. But OQ = r, so by the definition of inversion, P is the inverse of R. Hope this helps!
Sir pls tell what is 'inverse' ?? or some link explaining it :)
Log in to reply
Yes. Geometrical Inversion is a very powerful tool used in more advanced geometry problems. I am still not very good at it; it is basically a transformation of the plane. The reason for its power is that it preserves angles, and also has a lot of nice properties. Here is a link to get you started, although I think the best way is to do problems :) http://www.geometer.org/mathcircles/inversion.pdf
Log in to reply
Hmmm. These are all the theorems realted to circle
Power of P = AP × PB = OQ 2 - OP 2
OQ 2 - OP 2 = PQ 2 [ Since △ OPQ is a right triangle
Again, we observe △ OPQ ∼ △ ROQ So, PQ 2 = OP × PR Therefore, OP × PR = AP × PB
This implies that the points O , A , R , B are concyclic. So ∠ ARO = ∠ ARP = ∠ ABO
Since ∠ ABO =150°, ∠ ABO = ∠ BAO = 15°
So the answer is 15
What is power? Can you explain?
Log in to reply
He is referring to the power of a point. Search it up on Google and check the site "art of problem solving", it'll explain it well
I thought angle AOB is 150 not ABO
Brace yourselves.
Let the angles Q O P = α , A P R = β , A O R = γ , A R O = δ . We want to find δ and know that ∠ O A B = 1 5 (I'll omit degree signs).
Let's set the scale so that O Q = 1 . Then, from basic trigonometry, O P = cos α , O R = cos α 1 . From the law of sines for △ A O P , we get sin β = cos α sin 1 5 .
γ can be expressed easily from △ A O P as β − 1 5 .
From the law of cosines for △ A O R , we obtain A R 2 = 1 + cos 2 α 1 − 2 cos α cos γ = 1 + cos 2 α 1 − cos α 2 ( cos β cos 1 5 + sin β sin 1 5 ) using the identity for cos x + y ; we can further simplify it to A R 2 = 1 + cos 2 α 1 − cos α 2 ( cos β cos 1 5 + cos α sin 2 1 5 ) = 1 + cos 2 α 1 − 2 sin 2 1 5 − cos α 2 cos β cos 1 5 = 1 + cos 2 α cos 2 1 5 − sin 2 1 5 − cos α 2 cos β cos 1 5 .
Next step: law of sines again, for △ A O R . Using the expression for A R 2 , we get 1 + cos 2 α cos 3 0 − cos α 2 cos β cos 1 5 = sin 2 δ sin 2 γ = ( sin δ sin β cos 1 5 − cos β sin 1 5 ) 2 = ( cos α cos 1 5 − cos β ) 2 sin 2 δ sin 2 1 5 .
Expanding the right side, we get ( cos 2 α cos 2 1 5 + cos 2 β − cos α 2 cos 1 5 cos β ) 2 sin 2 δ sin 2 1 5 = ( cos 2 α cos 2 1 5 + 1 − sin 2 β − cos α 2 cos 1 5 cos β ) 2 sin 2 δ sin 2 1 5 = ( cos 2 α cos 2 1 5 − sin 2 1 5 + 1 − cos α 2 cos 1 5 cos β ) 2 sin 2 δ sin 2 1 5 ;
notice that we got the same expression as on the left side, just multiplied by sin 2 δ sin 2 1 5 . Since the left side is non-zero, we can divide by it and get sin 1 5 = sin δ ; it's clear that 0 ≤ δ ≤ 9 0 , so δ = 1 5 . The only significant angle was that 1 5 degree one, so this is easily generalizable.
Why do it nicely if you can use horrible analytics! :D
Let Q' be the reflection of Q across P, which is also, the other point of tangency from R. By POP and since OQRQ' is cyclic, BP</code>\cdot<code>PA=QP</code>\cdot<code>PQ'=OP</code>/cdot<code>PR, implying BOAR is cyclic by converse of POP. Therefore, ARB=ABO=(180-150)/2=</code>\boxed{15}<code>.
Geometric inversion is not necessary, but a property given by it is useful.
Notice that, with respect to the circle, P is the inverse of R and A is the inverse of itself. Hence we can use the similar triangle theorem in inversion to show that O A P is similar to O R A .
Therefore ∠ O A P = ∠ O R A . But since A O B is isosceles, ∠ O A P = 1 5 ∘ and therefore ∠ A R P = ∠ O R A = 1 5 ∘ .