Day 3: Just Enough Information
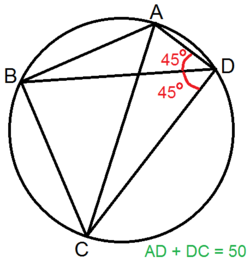
is a cyclic quadrilateral. . Also, .
Find the area of .
This problem is part of the Advent Calendar 2015 . This was inspired from a problem from the Kangaroo 2015!
The answer is 625.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Firstly ∠ A D C = ∠ A B C = 9 0 ∘ . Let A D = a , D C = b for clarity. Then the area of A D C = 2 1 a b .
As A B and B C subtend the same angle they are of equal length. So the area of A B C = 4 1 A C 2 , since if you construct the square with side A C , then it is clear that A B C has one quarter of that area.
So the area of A B C D = 4 1 A C 2 + 2 1 a b .
But A C 2 = a 2 + b 2 , so: A r e a o f A B C D = 4 1 ( a 2 + b 2 + 2 a b ) = 4 1 ( a + b ) 2 = 6 2 5
It is amazing that the area is independent of a and b ! Also for this to be a complete solution we must show that such a quadrilateral is possible; a square with sidelength 2 5 works perfectly.