Day 4: Cutting out Decorations

Geometry Level 2

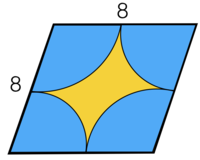A mathematician is cutting out an interesting star shape to use as a Christmas tree decoration. She cuts it out of a rhombus shaped card, and the rhombus has side-length 8. The star is made by cutting off circular sectors centered at each vertex that touch at the midpoints of the sides (as shown in the diagram above).

Find the perimeter of the star.

This problem is part of the Advent Calendar 2015 .
8 + 4 π 8 + 4\pi 24 24 12 π 12\pi 8 π 8\pi

View wiki
Michael Ng by Michael Ng , 22, United Kingdom

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

4 solutions

Michael Ng
Dec 3, 2015

The star's perimeter is equal to the total of the four sectors' perimeters. However since each sector has the same radius; 4 4 ; and since the total of the angles that the sectors create is precisely 36 0 ∘ 360^{\circ} , it follows that this perimeter is the same as the circumference of a circle of radius 4 4 .

Another way to see this is to tessellate this shapes and you will see a circle around every vertex.

Now the circumference of a circle of radius 4 4 is 2 π × 4 = 8 π . 2\pi \times 4 = \boxed{8\pi}.

15 Helpful 0 Interesting 0 Brilliant 0 Confused

Your incorrect to find area of star we need to find area of rhombus too and then we have to subtract the circle or else you will find the area after the star was removed

Aayush Patel - 5 years, 6 months ago

Log in to reply

Unfortunately the question asks for the perimeter of the star, otherwise you would be correct. Unlucky for misreading it!

Michael Ng - 5 years, 6 months ago

Perimeyer = 4 x arc length = perimeter of circle = 2pir - 2 x pi x 4 = 8 pi

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Let 4 angels of rohmbus is x,x and y,y and 2x+2y=360.
Now perimeter of each arc is 4x ,4x and 4y,4y.
Then perimeter of star is =4x+4x+4y+4y 4(x+x+y+y) 4(2pi)=8pi

Sagar Saha - 5 years, 6 months ago

One way to do this is to convert the rhombus into a square, then draw the star. We observed that the perimeter of the star is the perimeter of an inscribed circle in a square of side length 8 which is equivalent to 8 π 8\pi .

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Sanjam Singh
Dec 17, 2015

Lets take one circle: Radius=one side of rhombus÷2 =8÷2=4 units Peri=2 pi r =2× pi×4= 8 pi Peri of one quater circle=8÷4=2 pi Peri of four quater circle=peri of
star=4×2=8 pi

Solved

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...