Five Golden Circles
 Five congruent circles overlap. A line is drawn connecting the bottom of the first circle to the top of the fifth circle. The area enclosed by the circles under the line is shaded gold.
Five congruent circles overlap. A line is drawn connecting the bottom of the first circle to the top of the fifth circle. The area enclosed by the circles under the line is shaded gold.
The overlapping areas of two circles each have an area of 5, and the gold area is 35.
Find the area of one circle.
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
That is nice. I did not think of that. I just hit reveal solution after a short while :)
All that is right, I got the correct answer, assuming the total area was 35 x 2=70. But what if an algebraic proof was required to this assumption? Help required as I can't come up with anything
Genius solution !
same method
my bad English missed the question
Yessss!! :) i've done the same
I understand your answer but I'm thinking it's incorrect. I'll explain and possibly someone can tell me why I may be incorrect. The first half of the solution makes complete sense. However, the overlapping areas have an area of 5. You simply can't add the 4*5 back into the solution. Each overlap constitutes an area of 5 from BOTH circles that overlap. Meaning that each overlap equates to a total area of 10. So the solution should be 5C - 4 x 10 to get an area of 22 for each circle.
According to the statements, the answer can also be 14. First statement states that golden area all under the line. The intersection of circles is also supposed to be golden area. therefore total area = 35+35 = 70. Area of one circle = 70/5 = 14.
I believe the correct answer should be 16. The total area is indeed 70. But half of each of the overlaps is part of C. Only half represents a double count. So, the answer should be 5C -10 = 70. C = 16. To see another way, use symmetry. Exchange the yellow parts of the first two circles with the blue part of the fourth and fifth circles. Call each part of the non-intersecting part of the third circle A. By symmetry, these two parts are equal. Then 2C +A =35 and, for the third circle, 2A + 10 = C. Solve: A=3 and C = 16.
Same way except that I miscalculated and entered 2 0 and, in rage, hit the 'Reveal Solution' button :)
Suppose A is the area of a circle. Since all circles are congruent, the area of the light gold and gold must be 3 5 × 2 = 7 0 . The intersection area is 5 , then we get
( A − 5 ) + 5 + ( A − 1 0 ) + 5 + ( A − 1 0 ) + 5 + ( A − 1 0 ) + 5 + ( A − 5 ) = 7 0
5 A − 2 0 = 7 0
5 A = 9 0
A = 5 9 0 = 1 8
PERFECT ANSWER
Very elaborate
The area of the figure =2x35=70 then the area of the five circles= 70+4x5=90 then the area of one circle =90/5=18
Competitive way of doing.
pls tl me hw is it 2 x35 clearly
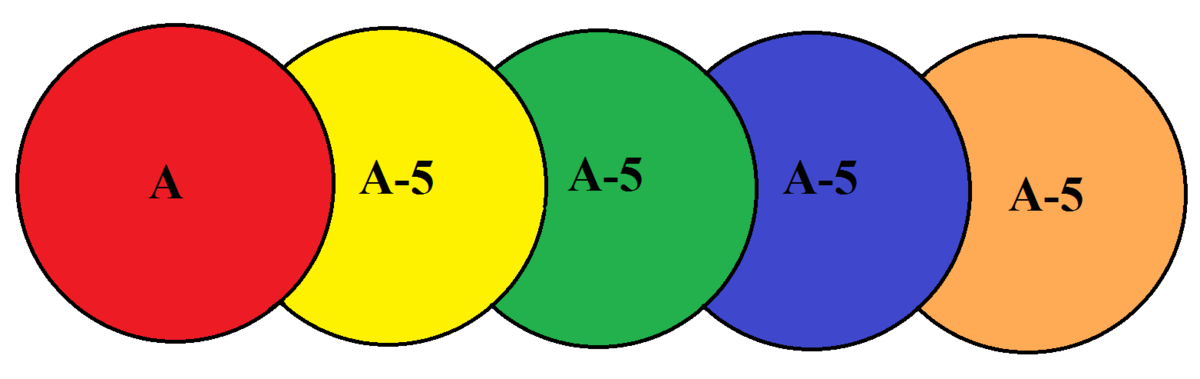 A
+
(
A
−
5
)
+
(
A
−
5
)
+
(
A
−
5
)
+
(
A
−
5
)
=
2
×
3
5
⇒
A
=
1
8
A
+
(
A
−
5
)
+
(
A
−
5
)
+
(
A
−
5
)
+
(
A
−
5
)
=
2
×
3
5
⇒
A
=
1
8
Most helpful n conceptual diagrams. The show.
Very helpful
Figure total area is 7 0 that is equal to 5 C − 4 I = 5 C − 4 ( 5 )
Solve
5 C − 4 ( 5 ) = 7 0
5 C = 9 0
C = 1 8
The golden area = the blue area = 35
Golden area + Blue area = 2x35 = 70
Area of 4 intersecting area = 4x5 = 20
Total area of 5 individual circles = 70+20 =90
Area of one circle = 90/5 = 18
To find the total area of the diagram, l multiplied the given area by 2 and got 7 0 . Since the circles overlap four times, 4 × 5 is the amount of overlap. Thus, without accounting for overlap the area is 9 0 which gives us an area of 1 8 for each circle since 5 9 0 = 1 8 .
I knew the total area was 70. Then I subtracted 20 for the overlapping parts. Then I imagined similar "overlapping" sections on the far left and far right circles so I subtracted another 10. This meant the "middle" section of each circle had to be 40/5 or 8. Then I added the 8 for the center of one circle plus 10 for the 2 overlapping pieces in one circle to get 18.
We are given the area under Line A which is from the bottom of the first circle to the top of the last and with this given information we can discover that the total area is double the golden area: G=Golden Area T=Total area, G=35 and 2G=T, so 70=T and since there is 4 equal overlaps in each circle and the area of each overlap is 5 so if we expand the figure to 5 tangent circles we had 4 over laps so the new area F=70+5(4)=90 and since we have 5 circles the area of a circle is Q=90/5=18
So the area of one of these circles is 18
Let the radius of each circle be 'r'. Then the common tangent below any two near circles is: √2 r so that the sides of the golden triangle are 4√2 r and 2r which gives us an expression for the golden area as :4 √2 r² + π r²/2 - 4[√2 r² -π r²/2 + 5/2] = 35 and A = π (r²). We get: r = 3√(2/π) and A = 18
Area of the circle = Ac Area of the overlapping thing =Ao We know that Ao is 5 so and and the golden area is 35 and if you look as all pieces together you see that this has an area of 2,5Ac -2Ao => 2,5Ac -2Ao=35 2,5Ac-10= 35 /+10 2,5Ac =45 /:2,5 Ac=18
I hope you can't understand that what Im trying to say. (I'm not an native speaker ;()
The golden area is 35 which is half of total area so total area is 70 no create same overlapping circles one before the first circle and second after the last circle now in total we will have 6 overlapping areas (convex lens shaped area) and 5 concave lens shaped area total area is 70 from which we know that 30 is taken by convex lens so 5 times the areaa of concave lens = 40 so area of one concave lens is 8 a circle is made up of one concave lens and 2 convex lens so 8+5+5=13
The total area is 7 0 . Now let the area of one circle be C . Then notice that the total area is 5 C − 4 × 5 as we have five circles minus four intersections.
Equating and solving gives C = 1 8 as required.