Day 5: Fixing Santa's Sleigh

Recall the divergence theorem:

$\int \int_S \, \vec{F} \cdot \, \vec{dS} = \int \int \int_V \, \nabla \cdot \vec{F} \, dV$

We want to find the left side (the flux). Conveniently, the divergence is a constant:

$\nabla \, \cdot \vec{F} = \frac{\partial}{\partial{x}} (3 x) + \frac{\partial}{\partial{y}} (3 y) + \frac{\partial}{\partial{z}} (2 z) = 3 + 3 + 2 = 8$

Put eight of the specified triangles together to form a closed surface, whose volume is that of two combined square pyramids (one upright and one inverted) of base side length $3 \sqrt{2}$ and height $4$ . The volume of this combined shape is $48$ . Integrating the divergence over the volume therefore yields:

$\int \int \int_V \, \nabla \cdot \vec{F} \, dV = 8 \int \int \int_V \,dV = 8 \times 48$

Due to symmetry, the flux over one of the eight sides (the original triangle) is therefore equal to $48$ .

Post-script: After messing up a similar problem by @Otto Bretscher today due to some silly mistakes, I'm glad to have been given a second chance :)

We are given that $\vec{F} \ = \ \begin{bmatrix} 3x \\ 3y \\ 2z \end{bmatrix}$ and a surface that is given by the equation $3z \ + \ 4y \ + \ 4x \ = \ 12$ . We know that we are solving an integral of the form:

$\displaystyle\int \displaystyle\int_C \ \vec{F} \ \cdot \ \nabla f \ \text{dA}$

This is because for some flux integral, we multiply $(||\nabla f||)\ \ \ \frac{\nabla f}{||\nabla f||} \ = \ \nabla f$ . We know that $f$ is going to be some function where $f \ = \ z \ - \ g(x, \ y)$ . We get that $f \ = \ z \ - \ 4 \ + \ \frac{4}{3}y \ + \ \frac{4}{3}x$ . By computing the gradient, we get $\nabla f \ = \ \begin{bmatrix} \frac{4}{3} \\ \frac{4}{3} \\ 1 \end{bmatrix}$ . We can then compute the dot product:

$\displaystyle\int \displaystyle\int_C \ \begin{bmatrix} 3x \\ 3y \\ 2z \end{bmatrix} \ \cdot \ \begin{bmatrix} \frac{4}{3} \\ \frac{4}{3} \\ 1 \end{bmatrix} \ \text{dA} \ \Rightarrow \ \displaystyle\int \displaystyle\int_C \ 4x \ + \ 4y \ + \ 2y \ \text{dA}\tag*{}$

We can substitute $z \ = \ g(x, \ y)$ back into the integral to get:

$\displaystyle\int \displaystyle\int_C \ 4x \ + \ 4y \ + \ 2(4 \ - \ \frac{4}{3}y \ - \ \frac{4}{3}x) \ \text{dA} \ \Rightarrow \ \displaystyle\int \displaystyle\int_C \ 4x \ + \ 4y \ + \ 8 \ - \ \frac{8}{3}y \ - \ \frac{8}{3}x \ \text{dA}\tag*{}$

We now must define the region of $C$ . We will say that $C$ lies on the $x-y$ coordinate plane, with $z \ = \ 0$ . The graph of the pipe's surface looks somewhat like this:

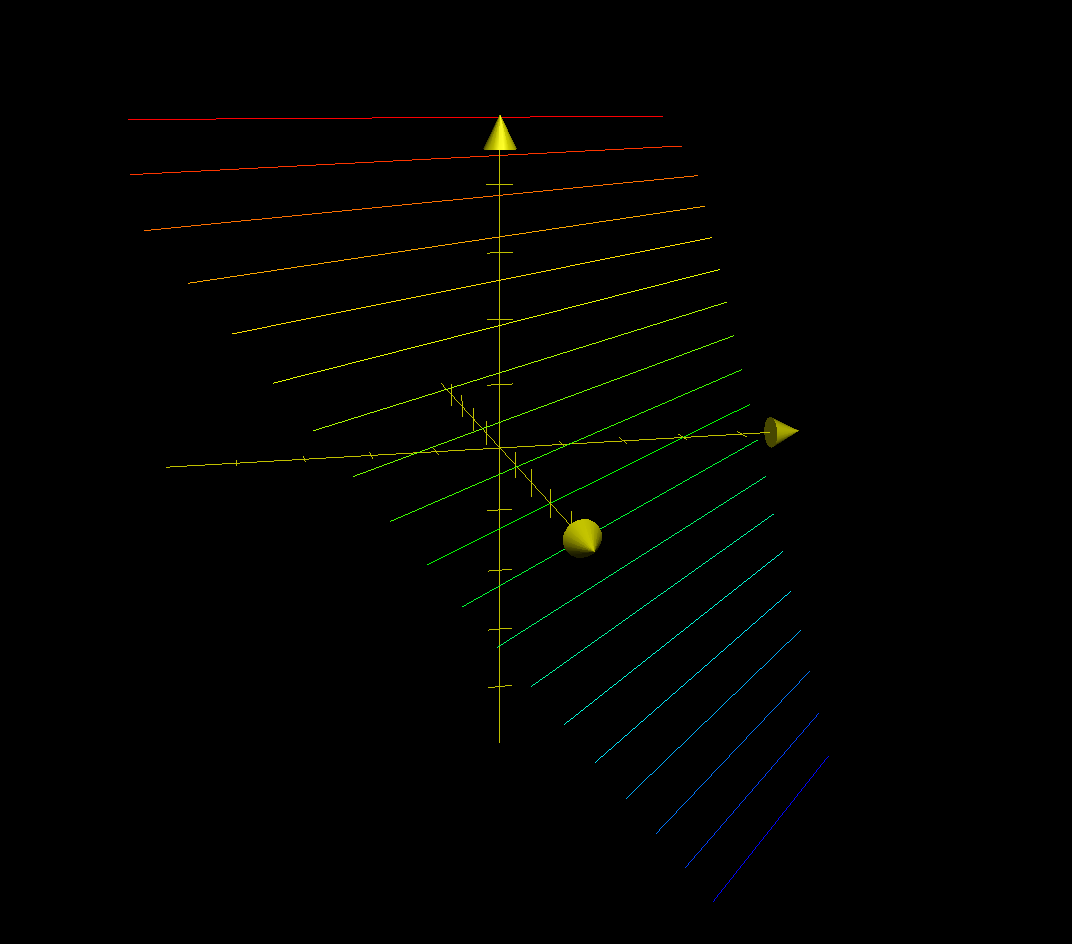
The surface intersects the $x$ -axis at $3$ and the $y$ -axis at $3$ as well. This means that to define $C$ we can vary $x$ between $0$ and $3$ , and we can vary $y$ between $0$ and $-x \ + \ 3$ , since the region is bounded by the $x$ -axis, the $y$ -axis, and the line with the equation $y \ = \ 3 \ - \ x$ . Setting up this integral:

$\displaystyle\int_{0}^{3} \displaystyle\int_{0}^{3-x} \ 4x \ + \ 4y \ + \ 8 \ - \ \frac{8}{3}y \ - \ \frac{8}{3}x \ \text{dy} \ \text{dx}\tag*{}$

We can now simply evaluate this integral fairly easily, and get the value of $48$ .