Day 7: Building a Snowman!
For the purposes of this question, we can assume that the geometric figures we are dealing with are two-dimensional.
Marcy is playing in the snow. After a long day of snowball fights and tobogganing, she decides to build a snowman with three snowballs. Marcy knows that the top snowball has a diameter of 4 units, and that the top two snowball masses are circular, while the bottom is an ellipse. In addition, Marcy pushes a long, straight tree branch into the snowman, from the midpoint on the bottom snowball's height, to the midpoint of the top snowball's height. She observes that it also intersects the middle snowball at the midpoint in its height as well, and that the twig makes an angle of 7 0 degrees with the horizontal at the intersection point on the bottom snowball. Finally, when Marcy disassembles the snowman, she notices that when she removes the middle snowball, keeping it at the same height (after removing the top snowball), and she drops it vertically, the snowball hits ground with a speed roughly equivalent to 2 0 times its radius.
Help Marcy to determine the sum of the two axes of the bottom snowball, to three significant figures.
Details and Assumptions
The snowballs are placed symmetrically on top of each other.
Take gravity to be equal to 1 0 m/s 2 . Energy transfer is 1 0 0 % efficient and there are no other external forces acting on the snowman.
This problem is part of The 12 Days of Math-Mas 2018
The answer is 18.4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
- The question asked for the sum of the axes, but your answer is based on the sum of the half axes.
Worth noting : Equalling both expressions for tan 7 0 ° : ( 2 1 c 2 + 2 c + 2 ) ( c − 2 ) = ( b − 2 ) ( c + 2 ) and plugging in b = a = 2 c 2 results in the identity: both sides evaluate to 2 1 c 3 + c 2 − 2 c − 4 . So a=b and the 'ellipse' becomes a circle.
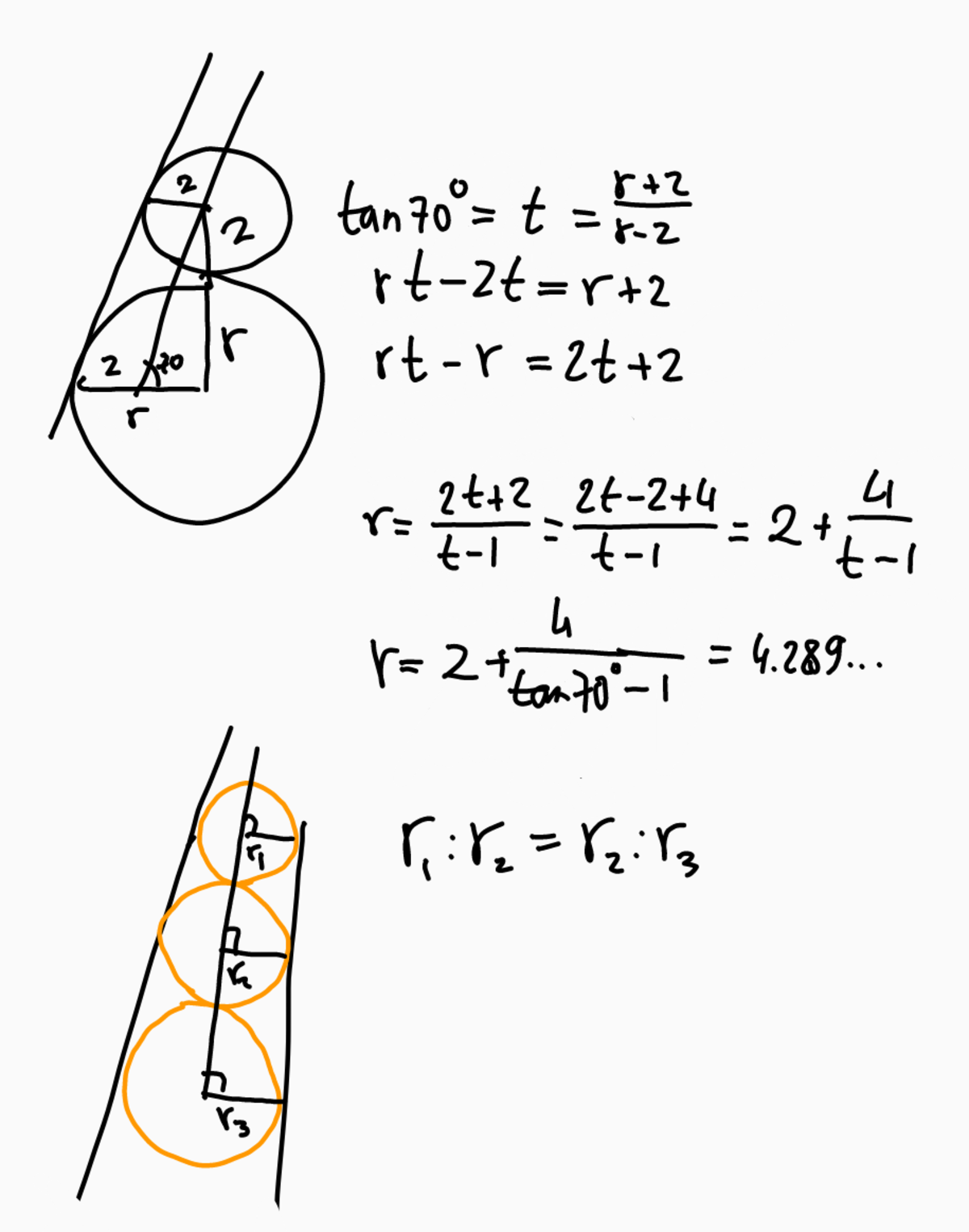 The top ball has radius 2.
The top ball has radius 2.
Let r be the radius of the middle bal. Calulate it using r − 2 r + 2 = tan 7 0 ° (see top picture), so that r = 2 + tan 7 0 ° − 1 4
If the (bottom of) the middle ball is at height h above the ground, conservation of energy implies m g h = 2 1 m v 2 ⇒ h = 2 g v 2 = 2 g ( r 2 0 ) 2 = g 1 0 r 2 = r 2 . Hence the vertical diameter d of the lower ball is also this value: d = h = r 2
The respective ball diameters 4 , 2 r , r 2 form a geometric progression, the lower ball would have exactly this same diameter if it was a sphere (see lower picture). Hence we conclude it must actually be a sphere.
The sum of the axes then is 2 d = 2 r 2 = 2 ( 2 + tan 7 0 ° − 1 4 ) 2 = 3 6 . 7 9 . . .
Some remarks
- After this answer was counted as 'incorrect', I suspected that maybe the expected answer was the sum of the half axes, and entered 1 8 . 4 on my second try, which was counted as 'correct'.
- The meaning of 'midpoint of/in the height' of a ball was at first unclear to me. After making the assumption that it referred to its top or highest point, I made some fruitless drawing efforts. Finally I understood that its side was meant, at the height of the centre.
- Since it does not matter where a line makes an angle with the horizontal, that added to my confusion, because it made me wonder if maybe something else was intended.
- Approximating g = 1 0 is far too course for 3- digit precision.
Assumptions I further had to make
- The symmetry mentioned is a vertical symmetry, and thus the stack is vertical and the lower ball's main axes are horizontal and vertical.
- The 'unit' used is a metre, this matters because the value of g depends on it .
- Marcy is superhuman, making snowballs of several tonnes after a long day of snowball fights and tobogganing.
Hey - So sorry about any confusion, I'm going to try to change the wording of the question to make it more clear.
That is nice of you, thanks for the response!
We start by making a diagram to help us clarify the situation:
The image isn't amazing, but assume that the line is at an angle of 7 0 degrees to the horizontal, and that the point that in intersects each of the circles/ellipses is the midpoint of the height (vertical diameter) of the geometric figure. We can see that in this image, we have two similar right-angled triangles with defined angles. We can now start to define the sides of these triangles in terms of the different circle/ellipse axes. For the larger triangle, we know that the base will be equal to the value b − 2 , since the length is the same as the distance from the endpoint of the top circle's radius to the end of the ellipse's long axis. We can calculate the height of this triangle by realizing that it is equal to the short axis a of the ellipse, plus the diameter of the middle circle, plus 2 . We can find the value of the middle circle's diameter fairly easily using the given information about the velocity of the snowball just before it hits the ground. At this point, with no external forces and 1 0 0 % energy efficiency, all gravitational potential energy should become kinetic, so we get: m g h = 2 1 m v 2 ⇒ 2 0 h = v . This means that the radius of the circle must be equal to h , or c 2 = h . We also know that a = 2 h , so a = 2 c 2 . We know know that the height of the larger triangle is 2 c 2 + 2 c + 2 and the base is b − 2 . We know that one of the angles of the triangle is 7 0 degrees, so we get:
tan 7 0 ° = b − 2 2 c 2 + 2 c + 2
For the smaller triangle, we follow a similar process, finding that the height is equal to c + 2 , and the base is equal to c − 2 . We now get:
tan 7 0 ° = c − 2 c + 2
We can solve the second equation for c , then plug it into the first equation to get b . Finally, we know that a = 2 c 2 , so when we take the sum of the values obtained, we get 1 8 . 4 .