Day 7: The Seven Eggs

The condition means that we can only get groups of $1$ and $2$ consecutive eggs.

If the seven eggs were grouped $1, 1, 1, 1, 1, 1, 1$ , then how many ways are there to arrange them? We can model an arrangement by its gaps between each group. There are $6$ positive gaps and two non-negative gaps on either side. We also know that the total number of gaps is $15-7=8$ . Now we add one to each non-negative gap to make them positive.

Now by 'stars and bars' we have $8$ variables which total $10$ , giving us $\binom{9}{7} =36$ ways.

We continue similarly for $2, 1, 1, 1, 1, 1$ ; we have $\binom{9}{6}$ ways. However then we can permute the twos and ones giving $\binom{9}{6} \times \binom{6}{1} =504$ .

For two twos we get $1260$ ways and for three twos we get $504$ ways, giving us a total of $\boxed{2304}$ .

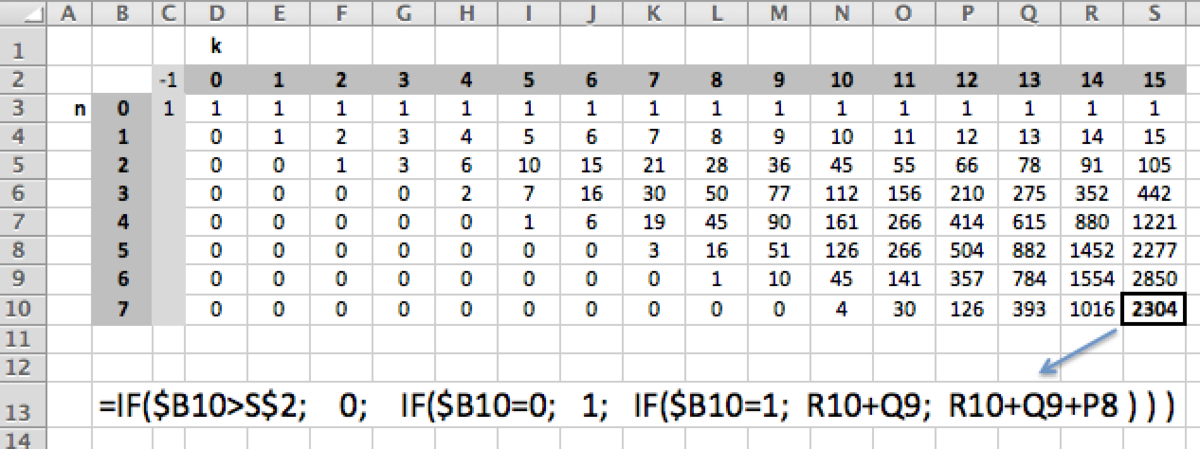
For $n$ places and $k$ eggs, let $S_k(n)$ be the number of ways to do it. You can either:

• start with no egg, so you have $S_{k-1}(n)$ possibilities;
• start with an egg, then no egg, so you have $S_{k-2}(n-1)$ possibilities;
• start with two eggs, then no egg, so you have $S_{k-3}(n-2)$ possibilities.

This gives a recursive relation :

$\boxed{S_k(n)=S_{k-1}(n)+S_{k-2}(n-1)+S_{k-3}(n-2)}$

With $S_k(0)=1, \forall k$ , and $S_k(n)=0$ when $n>k$ or $n<0$ .

Easy to put in a program or in a spreadsheet:

# Python code
def S(n,k):
    if n == 0:
        return 1
    if n > k:
        return 0
    if n < 0:
        return 0
    return S(n,k-1) + S(n-1,k-2) + S(n-2,k-3)

print S(7,15)
>>> 2304

Let $A(n,k),B(n,k),C(n,k),D(n,k)$ denote the number of arrangements with $k$ eggs and $n$ egg-holders with last two places of the arrangements being $\_\hspace{2pt} \_,\_ \hspace{2pt} E,E \hspace{2pt} \_$ and $E \hspace{2pt} E$ respectively. Here $E$ means an egg is present at a place and $\_$ means the place is empty.

Now for $i\geq 3, j\geq 1$ we have the following recursive equations : $A(i,j)=A(i-1,j)+C(i-1,j)\\ B(i,j)=A(i-1,j-1)+C(i-1,j-1)\\ C(i,j)=B(i-1,j)+D(i-1,j)\\ D(i,j)=B(i-1,j-1)$ and the following boundary conditions : $A(2,0)=B(2,1)=C(2,1)=D(2,2)=1$ apart from the above, we have $A(2,\cdot)=B(2,\cdot)=C(2,\cdot)=D(2,\cdot)=0$ .

We also have $A(i,0)=1, B(i,0)=C(i,0)=D(i,0)=0, \hspace{10pt}\forall i\geq 2$ Hence the recursion is now fully specified. We need $A(15,7)+B(15,7)+C(15,7)+D(15,7)=2304$

There are 4 possible solution cases for the spaces between the eggs, and 4 possible main cases for egg distribution.

Solutions for spaces between the eggs 1. There are eggs at the end 2.The left end has no egg 3.The right end has no egg 4. Both ends have no egg.

The sum for spaces between eggs or egg pairs. is that of identical objects into distinct bins where the bins are not empty, to ensure that the separate cases for pairs hold for no eggs at end, the two cases of only one egg at the end, and that of both eggs at the end.

Checking the handy identities for binomial coefficients, this reduces too

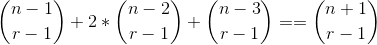
Cases for eggs

1. No pairs

There is only one possible combination 2. One pair There are 6!/(5!) or 6 combinations 3. Two pairs

There are 5!(3!*2!), or 10 combionations. 4. Three Pairs

There are 4!/(3!), or 4 combinations.

Multiply the above formula with the separate cases and sum.