Day Clock
You have a day clock, which in addition to being a regular 12 hour clock with an hour hand and a minute hand, also has a day hand and markings at regular intervals to show what day of the week it is. If the day hand and the hour hand are superimposed on Sunday at noon, what time on Friday morning will the day hand and hour hand be superimposed?
Round your answer to the nearest minute, and express your answer without the colon. For example, if you think the answer is 6:45 am, type in 645.
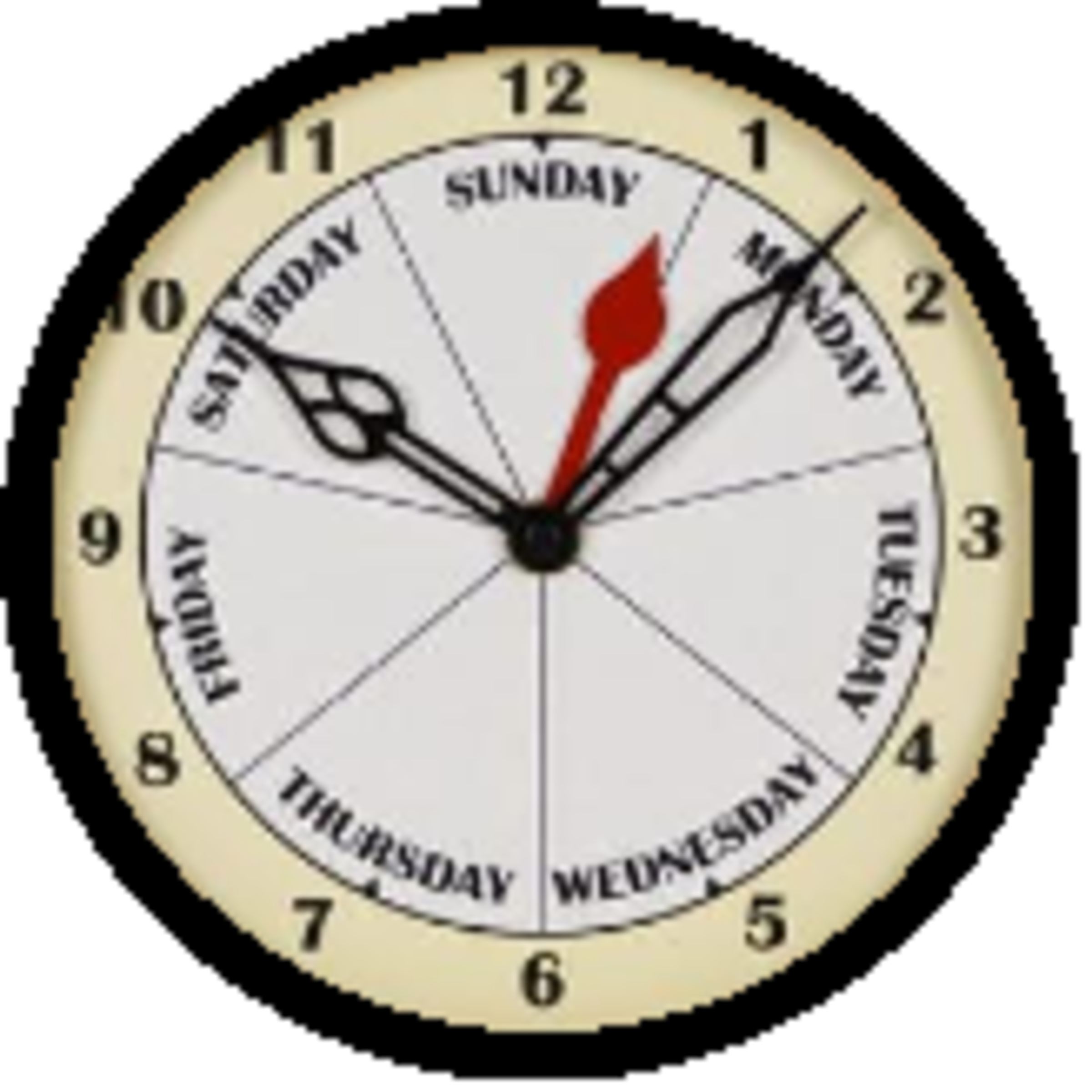
The answer is 818.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Hi there, David Vreken. Your solution is much more elegant than the approach I used this time. Though I must admit I came up with an equivalent approach on my own to determine when the minute and hour hands overlap on a regular clock in an attempt to give my nephew a learning experience with division. Anyway, thanks for sharing!
Let 1 unit be equal to 6 π radians. I set up the equation (1 unit/hour)t = [(12 unit)/((24)(7) hour)]t+12k. This simplifies to t = 1 4 1 t + 1 2 k . I manipulated the equation to say 1 4 1 t = 1 3 1 2 k . Note that 1 4 1 t is the number of units the day hand moves in t hours. We want this number of units to occur on a Friday, which is between 4.5 and 5.5 days from noon Sunday. Converting days the day hand moves to units gives 4 . 5 ⋅ 7 1 2 units and 5 . 5 ⋅ 7 1 2 units. So, we want 4 . 5 ⋅ 7 1 2 < 1 4 1 t < 5 . 5 ⋅ 7 1 2 . Since 1 4 1 t = 1 3 1 2 k , we can write 4 . 5 ⋅ 7 1 2 < 1 3 1 2 k < 5 . 5 ⋅ 7 1 2 ⇔ 8 1 4 5 < k < 9 7 3 . The only integer k inside this interval is k = 9 . Solving the equation, t = 1 4 1 t + 1 2 k , with k = 9 results in t = 1 3 1 4 ⋅ 1 0 8 = 8 1 3 4 . Convert 1 3 4 to minutes by multiplying by 6 0 , and you will get the final answer 8:18.
From Sunday noon to the next Sunday noon, the hour hand will pass the day hand 2 ⋅ 7 − 1 = 1 3 times over a period of 2 4 ⋅ 7 = 1 6 8 hours. Therefore, the day hand and the hour hand will be superimposed every 1 3 1 6 8 hours, and if n is the number of times that the hands are superimposed since Sunday noon, and h is the number of hours since Sunday noon, then h = 1 3 1 6 8 n .
Friday is 5 days after Sunday, so Friday noon is 5 ⋅ 2 4 = 1 2 0 hours after Sunday noon, and Friday morning would start 1 2 0 − 1 2 = 1 0 8 hours after Sunday noon. Therefore, the superimposed hands must occur between h = 1 0 8 hours and h = 1 2 0 hours, so 1 0 8 < 1 3 1 6 8 n < 1 2 0 , which means 8 1 4 5 < n < 9 7 2 , and since n is an integer, n = 9 (which means Friday morning is the ninth time in the week that the hands are superimposed).
Since n = 9 for the superimposed hands on Friday morning, the number of hours since Sunday noon is h = 1 3 1 6 8 n = 1 3 1 6 8 ⋅ 9 = 1 1 6 1 3 4 . Since Friday starts at 1 0 8 hours after Sunday noon, the hands are superimposed 1 1 6 1 3 4 − 1 0 8 = 8 1 3 4 hours into Friday morning. And since 1 3 4 of an hour is 1 3 4 ⋅ 6 0 ≈ 1 8 minutes, the hands are superimposed at approximately 8:18 am on Friday morning, which would be entered as 8 1 8 with the given instructions.