10 of 100: Parallel Puzzle
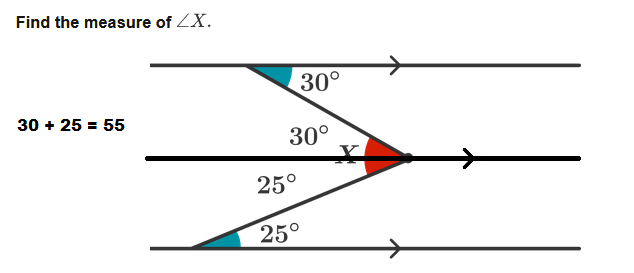
Find the measure of ∠ X .
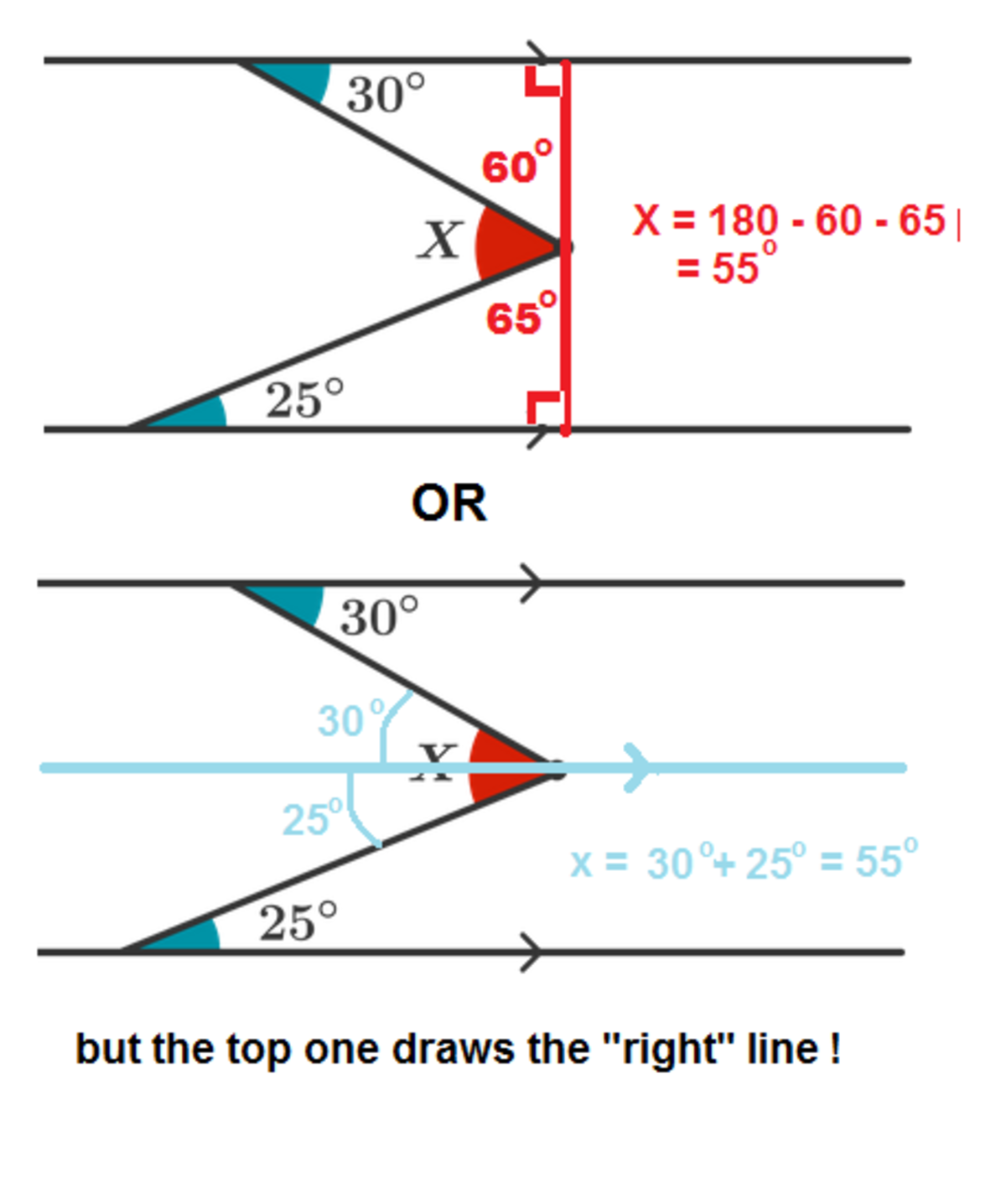
This problem can be solved in moments if you draw in just the right line!
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
20 solutions
Due to alternate angles in parallel lines(just thought it'd be good to explain how I think Karl Snowsill got his answer)
When I was at school that were called Z angles of the set 'FUZ' which all contained similar angles. Does anyone want to do a rotation animation?
Wish I thought of that! 😁 thumbs up 👍 for you
'Z' angles are another name for alternate angles, Karl Snowsill, probably due to the shape created when a line is drawn to intersect two parallel lines.
Pretty neat! I didn't think about it that way, but dropped a perpendicular to both of the parallel lines and did some calculations. Thank you for posting this :D
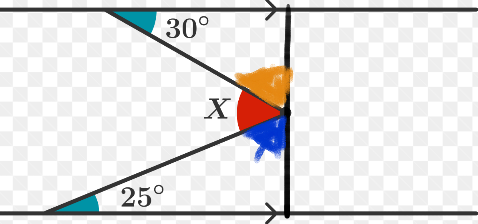
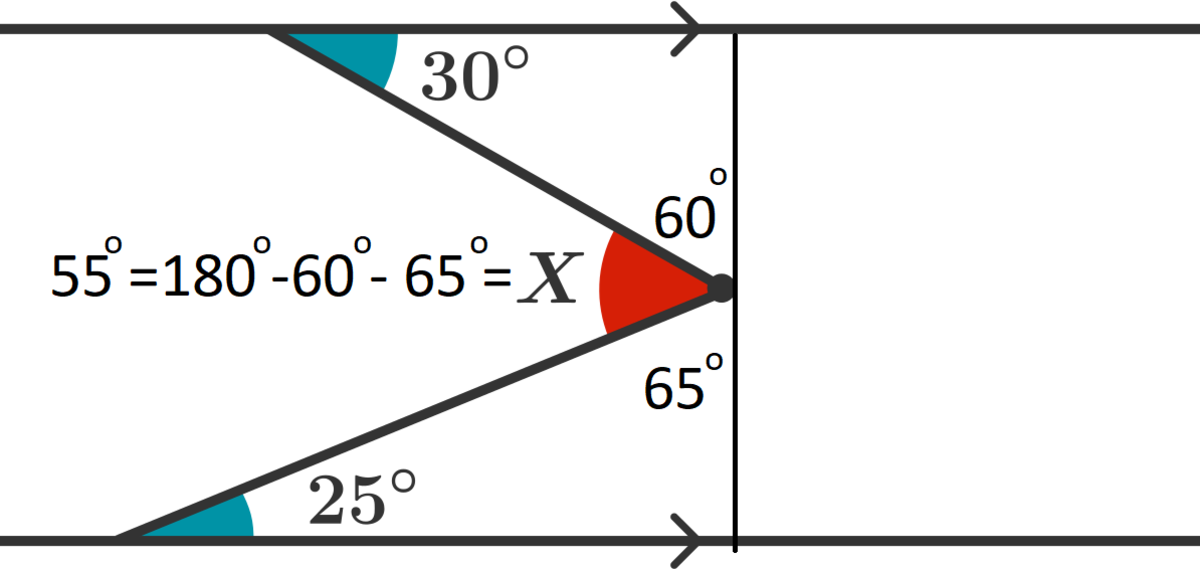
Here orange angle is 60 degree and blue angle is 65 degree.
So x=(180-60-65)= 55 degree
I solved it the same.
How do you know that the orange is 60 and blue is 65?
Log in to reply
adding the line creates a 90 degree angle, 1 triangle when it has it's angles added up it equals 180, 180-90=90, to get the angle for blue do 90-25=65 and to get orange do 90-30=60. blue, orange and red added up will equal 180 (because it is the angle of a straight line) so if you add 65 and 60 you get 125. 180-125 equals 55 degrees. (Hope this helped).
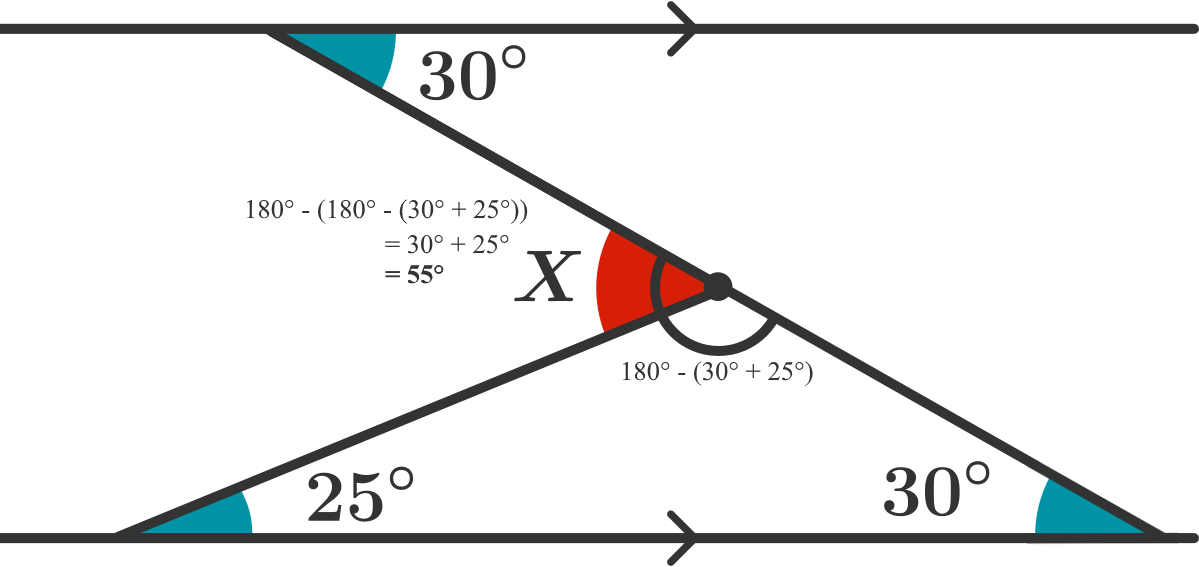
wont it be esiar to just add 25 to 30 to get 55?
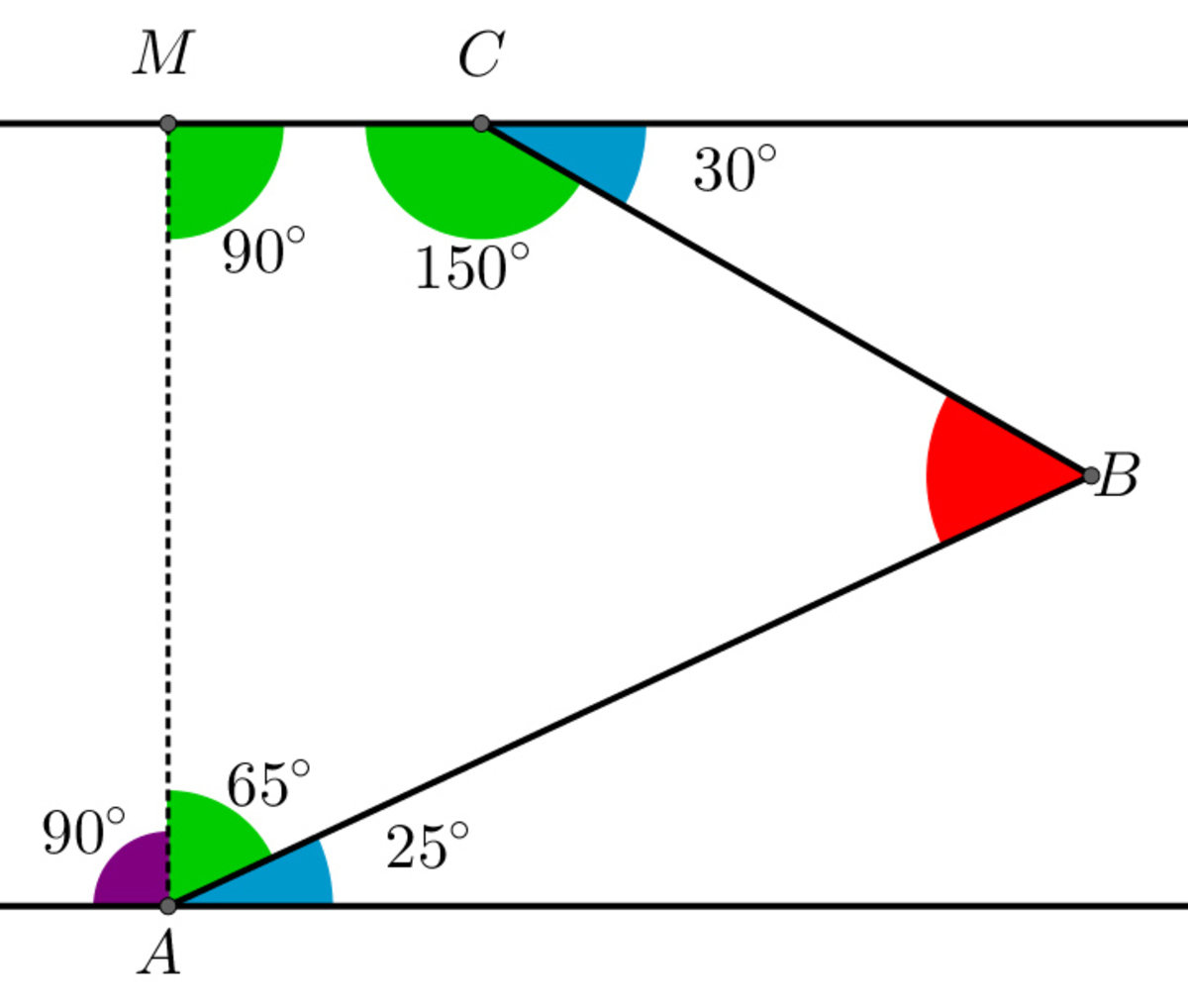
You can also skip computing for the third interior angle if you know Euclid's Elements I.32 (exterior angle = sum of opposite interior angles)
Let
M
be a point of the top line, so that
A
M
C
∠
=
9
0
°
. Since the two line is parallel,
B
A
M
∠
=
(
1
8
0
°
−
2
5
°
)
−
9
0
°
=
6
5
°
. We also know that
B
C
M
∠
=
1
8
0
°
−
3
0
°
=
1
5
0
°
. In a quadrilateral the amount of the angles is
3
6
0
°
, so
A
B
C
∠
=
3
6
0
°
−
6
5
°
−
9
0
°
−
1
5
0
°
=
5
5
°
.
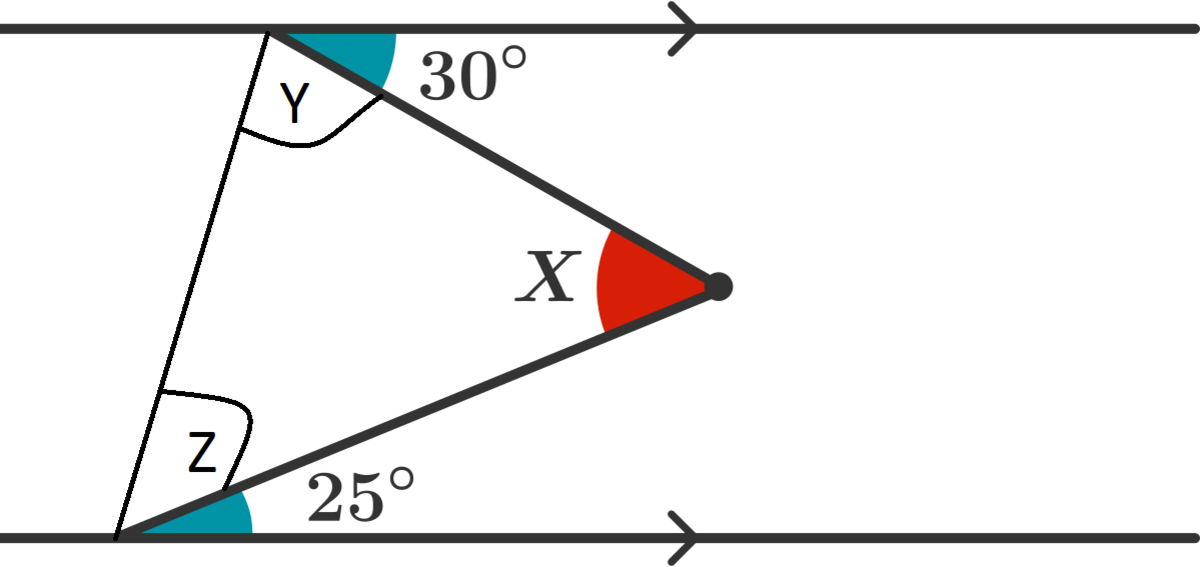 Using line to connect both line:
Using line to connect both line:
Y + Z + 30 + 25 = 180
And X + Y + Z = 180
Hence X = 55
Wow. How did I not see that!?
if we make a triangle with the 30 degree and 25 degree. the outer angles are 60 degree and 65 degree.
so,180-(60+65)=55. so the answer is 55 degree.
nice solution.
thanks.your comment inspired me
add 25 degrees + 30
Starting from the top line:
Each blue angle represents a clockwise rotation of the previous line, and the red angle is a counter clockwise rotation.
In order for the original line to end up parallel to itself, the amounts of clockwise and counter clockwise rotation have to be equal (or in other cases add to a multiple of 180º).
Thus, X = 25º + 30º = 55º
I just thought intuitively about it, if we slide the middle point vertically up we will end up with that shape
 from here we can solve it easily as x = 55
from here we can solve it easily as x = 55
I did it by constructing a straight line creating two right triangles. Since every triangle = 180° , and the angles about a straight line are 180° , by subtraction, one gets 55°
The slope of the line produced by the 25° angle is t a n ( 2 5 ° ) , while the slope of the line produced by the 30° angle is - t a n ( 3 0 ° ) . The angle between two lines of slope u and v is t a n ( m ) = 1 + u × v u − v , therefore our angle of choice is X = a r c t a n ( 1 − t a n ( 2 5 ° ) × t a n ( 3 0 ° ) t a n ( 2 5 ° ) + t a n ( 3 0 ° ) ) which computes to 55°.
L
a
T
e
X
Draw an auxiliary line parallel to the given two passing through "the point corresponding to the X angle". The angle gets divided in two parts whose value we can get by thinking about alternate interior angles (highlighted in the picture)
I drew a line perpendicular to the parallel lines at the intersection of the two lines that form 25 degrees. This created an irregular quadrilateral, which obviously has 360 degrees as the sum of internal angles. 90-25=65 degrees is the bottom angle. 90 degrees is the angle in the top left hand corner (perpendicular lines). 180-30=150 degrees as the top right angle. 65+90+150=305 and 360-305=55 degrees.
Sum of alternates.
Parallelity is why.
Fifty-Five is sum.
While I appreciate the haiku, I don't think this one's 100% clear without a picture.
Do you think that any solution to such a problem requires a picture? Or just that my solution could be written better?
extending either existing line segment through point x to the second parallel line gives solution quickly