12 of 100: Winding Roads
In which figure is the black path the shortest ?
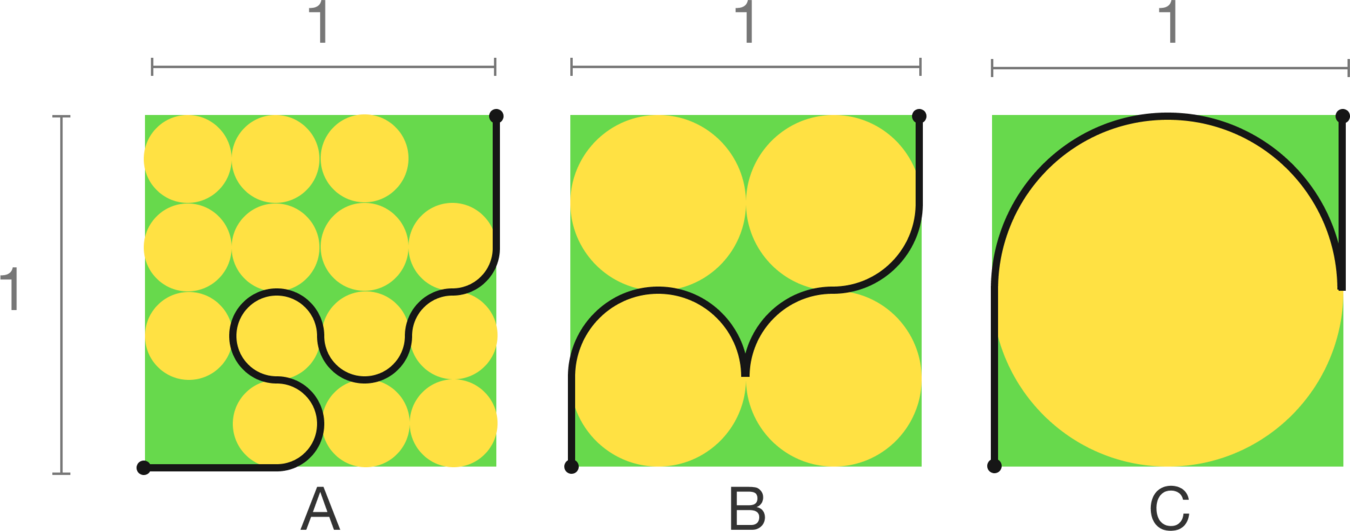
There are some quick-and-clever solutions where the path lengths are carefully compared but never calculated. However, most who guess at a glance guess wrong.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
18 solutions
Oopsy! Sorry I mixed up the colors at the top :)
I got to the values, but when I was comparing two of them, I stopped thinking and unwittingly chose the longer path. :/ (Is there a reward for doing all 101 questions right? I'm just asking.)
Tabulated:
| Fig | Diameter | Circumference | Circular Paths | Circular Length | Straight Length | Total |
| A | 4 1 | 4 1 ∗ π | 2 4 1 or 4 9 | 1 6 9 ∗ π | 4 3 | 4 3 + 1 6 9 π |
| B | 2 1 | 2 1 ∗ π | 1 | 2 1 ∗ π | 1 / 2 | 2 1 + 2 1 π |
| C | 1 | π | 2 1 | 2 1 ∗ π | 1 | 1 + 2 1 π |
Comparing them without multiplying the pi, the answer is B .
Let, S, M, L be the circumference of small, medium and large circle respectively. Ds, Dm, Dl are their diameters.
For A, total path= Ds + 1/2 Ds + 1/2 S + 3/4 S + 1/2 S + 1/4 S + 1/4 S + Ds + Ds = ( 3 Ds + 9/4 S ) = 3/4 + 9pi/16.
For B, total path= 1/2 Dm + 1/2 M + 1/4 M + 1/4 M + 1/2 Dm = ( M + Dm ) = 1/2 + pi/2.
For C, total path= 1/2 Dl + 1/2 L + 1/2 Dl = ( Dl + 1/2 L ) = 1 + pi/2.
so, we can see total path length of B is the smallest of them! Answer: B
Still waiting for the solution mentioned in the NOTE.
I just can't believe I selected the longest instead of the shortest...
I thought about the fact that to get from the bottom-left corner to upper right-corner, you need to travel 1 unit to the right and 1 unit up. Once you consider this, you can consider how much movement back (left/right, up/down) the path takes in 1/2 and 1/4 unit increments. It's clear from this that (B) is the correct answer.
I like your solution
Since the circles in each figure have different radius, why the curved surfaces would not count?
Log in to reply
They would count. This answer works in this case but it just happens the approximation is close enough; if it was tighter this method could fail.
I understood after I saw this example
I would like to point out though that this method will bound to fail if we are dealing with tighter and more tricky problems.
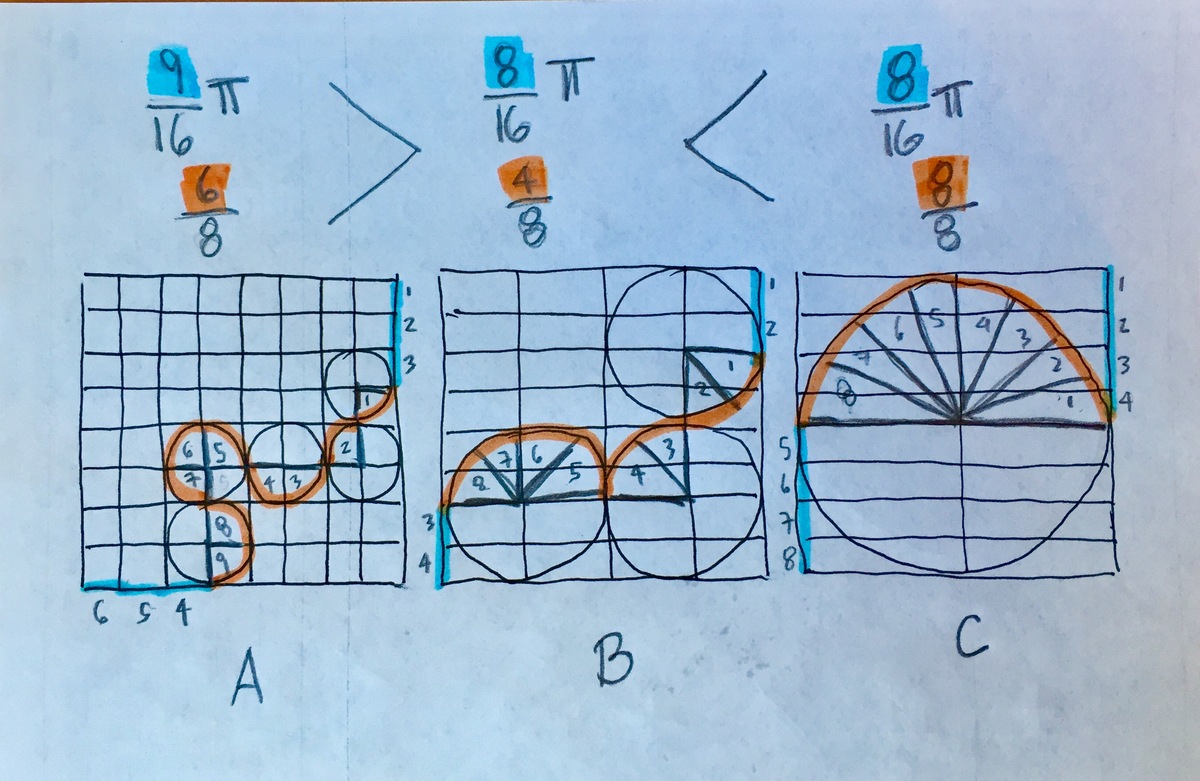
For A we pass through 9 quarter arcs. For B we pass through 4 quarter arcs. For C we pass through 2 quarter arcs. Since arc length and radius are both linear measurements, they are proportional, so those numbers can be converted to the same units: A = 2.25 small circles B = 2 small circles (= 8 small quarter circles) C = 2 small circles (= 8 small quarter circles) So no we need to compare the straight lengths: A = 6/8 = 0.75 B = 0.5 C = 1
So total size: A = 2.25c + 0.75 B = 2c + 0.5 C = 2c + 1
Therefore, B is smallest, without using pi at all.
Which is longest requires a bit more work...
Noting that the diameter and circumference of a circle in figure C is 4 times as much as a circle's diameter and circumference in figure A and that the diameter and circumference of a circle in figure B is twice as much as a circle's diameter and circumference in figure A, we have the following:
Figure C
- Total Circular Path : 1/2 the circumference of a circle in C which is equivalent to twice the circumference of circle in figure A;
- Total Straight Path : a diameter of a circle in C, which is equivalent to 4 times the diameter of a circle in A.
Figure B
- Total Circular Path : a circumference of a circle in B which is equivalent to twice the circumference of a circle in A;
- Total Straight Path : a diameter of a circle in B, which is equivalent to twice the diameter of a circle in A.
Figure A
- Total Circular Path : 2 and a quarter circumferences of a circle in A;
- Total Straight Path : 3 times the diameter of a circle in A.
Figures C and B have the same total circular path of twice the circumference of a circle in A, but Figure C twice the total straight path of that in figure B so, the total path in figure B is shorter than that of figure C. Figure A has both a greater total circular path and total straight path than that of figure B.
Hence, Figure B has the shortest distance.
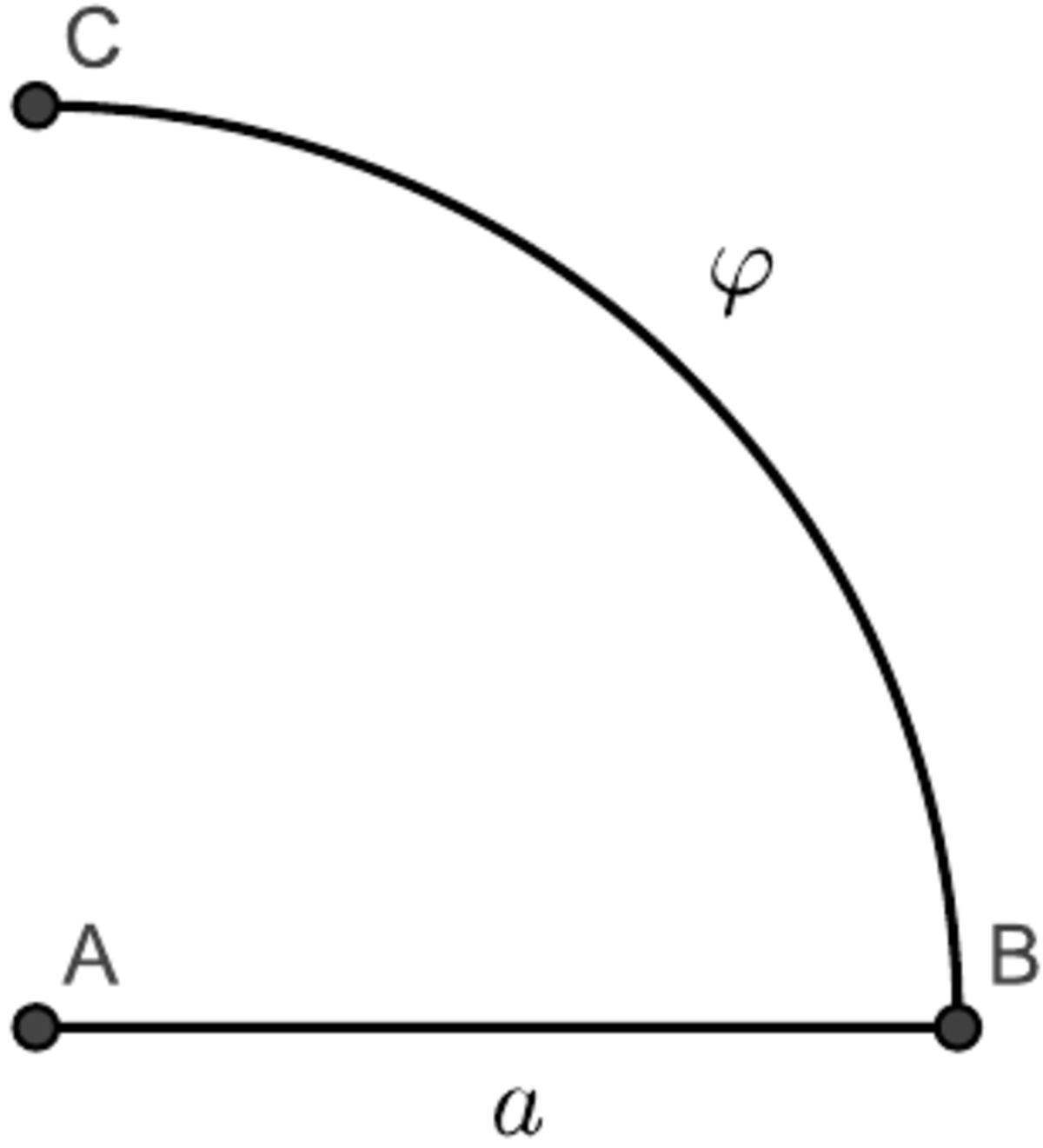 As we know,
φ
(
k
a
)
=
k
φ
(
a
)
, because of
C
=
2
π
r
(look at picture above).
As we know,
φ
(
k
a
)
=
k
φ
(
a
)
, because of
C
=
2
π
r
(look at picture above).
Let a 0 = 8 1 (radius of lowest circle), φ ( a 0 ) = φ 0 , ℓ i — length of line on each picture.
Then:
- a = a 0 , ℓ 1 = 6 a 0 + 9 φ 0 .
- a = 2 a 0 , ℓ 2 = 2 a + 4 φ ( a ) = 4 a 0 + 8 φ 0 .
- a = 4 a 0 , ℓ 3 = 2 a + 2 φ ( a ) = 8 a 0 + 8 φ 0 .
Therefore ℓ 1 = ℓ 2 + 2 a 0 + φ 0 and ℓ 3 = ℓ 2 + 4 a 0 .
So we can say, that ℓ 2 is shortest.
This solution doesn't differ from others, it just use other symbols.
The basic idea is to get from one corner to the opposite one. All the figures are possible and cover the same distance. B is the only direct one going through the different points only once.
If we double/halve the radius, the perimeter doubles/halves too. By moving pieces of the black path, we get:
A: 9 / 4 of small size circles + 1 - 2 radius of small size circles = 9 / 8 of medium size circles + 1 - 1 radius of medium size circles
B: 1 medium size circle + 1 - 2 radius of medium size circles
C: 1 / 2 of large size circle + 1 = 1 medium size circle + 1
Hence B is the shortest path
Well, you shouldn't say paths are never calculated. The solutions below just did that, and corretly. that's the righteous way to solve - calculating (pi is a value - whether you represent the letter or the number, it's already a value and part of a calculation...)
Just because none of us posted such a solution doesn't mean there isn't one. I certainly did not see any way to find the answer without dealing with the actual distances and some calculation.
My contribution minimally calculates the straight and arc distances to the point where the relationship of all three is quite obvious but never computes that actual distances, pi remains only a symbol, and thus never needs a calculator.
I await our puzzle masters showing us how the result follows without using quantities at all, as suggested by the text to which you rightly object.
lol pi is not a symbol, pi is a value. You can answer with pi, eve more because there is no more correct way to answer than with. if you pick 3,14 instead of pi, the earth would be collapsed when it dodges the Translational ellipse
I await the clever solution that in no sense calculates.
However, I found it simplest to count the linear and circle arc lengths separately using the circle radii to get the former. In the smaller circle examples I counted quarter circumferences to more easily track the paths that only went a quarter circle or a three quarter circle.
A 3/4 + 9 quarter arcs. diameter = 1/4, quarter circle = π/16. Total: 3/4 + 9π/16
B 1/2 + 4 quarter arcs. diameter = 1/2, quarter circle = π/8. Total: 1/2 + π/2
C 1 + 2 quarter arcs. diameter = 1, quarter circle = π/4. Total: 1 + π/2
It is immediately apparent that B is the smallest with less linear distance and no more than equal arc distance.
It is also not difficult to see that C is the longest since the additional 1/4 linear distance beats the π/16 < 4/16 = 1/4 additional arc distance of A.
Check out Cary Sabados' solution.
I was able to do this by eyeballing and comparing the three.
B looks the most like a straight line connecting the two corners, so this could be used to quickly determine that it is probably the shortest path.
Let
a
=
radius of one of the circles in
A
.
Length of square
=
8
a
.
Path
A
=
3
a
+
π
a
+
π
a
+
π
a
+
2
π
a
+
2
π
a
+
3
a
Path
A
=
6
a
+
4
π
a
Path
A
=
2
a
(
2
π
+
3
)
Path
B
=
2
a
+
2
π
a
+
2
π
a
+
2
a
Path
B
=
4
a
+
4
π
a
Path
B
=
2
a
(
2
π
+
2
Path
C
=
4
a
+
4
π
a
+
4
a
Path
C
=
8
a
+
4
π
a
Path
C
=
2
a
(
2
π
+
4
)
It can be seen that Path
B
is the shortest path.
Q.E.D
LaTeX: Thus, the shortest pink path is : B
Think about it this way:
-You have to displace 1 unit up somehow
-You have to displace 1 unit right somehow
The more you backtrack, the longer your distance
In A you back track in every turn (either up/down or left/right) In B you back track only once In C you also back track once as well but it seem longer than the one in figure B
But still, finding the actual distance it the best way to go
I thought how the lines would look if cut into straight lines.Doing this allowed me to reason out what line was longest (A) and just do the same and eliminate other options.
Simple solution, with little calculation:
Say an "arc" is 1/2 * circumference of circle. (a half-circle)
So I called "Arc1" the arc length of the circle with circumference = 1 (the circle in C). Arc1 = 0.5(r2pi) = r*pi = pi/2. Since the radius halves and quarters in B and C, for circles w/halved and quartered radii, Arc2 = pi/4 and Arc3 = pi/8.
Form there, simply count arc lengths. The arcs add up to the equivalent of 2*Arc1.
BUT, you also add a (line) in C, a (line minus a bigger gap thing) in B, and a (line minus a smaller gap thing) in A. Without even doing the (more thorough) geometry math, you know that 2*Arc 1 + (1 minus the bigger gap) is the smallest number of the three. Thus, B has the shortest path.