14 of 100: Red Dot Fever
In the image above, 3 dots from the grid (marked red) lie on the hypotenuse of a right triangle. If the corners of the triangle were instead at ( 0 , 0 ) , ( 1 2 0 0 , 0 ) , and ( 1 2 0 0 , 1 0 0 0 ) , how many dots from the grid would lie on the triangle's hypotenuse?
If you don't know where to start, try hunting for a pattern with smaller examples!
The answer is 201.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
20 solutions
Moderator note:
Here's this specific solution with generalization substituted in, to make it easy to compare in parallel. (Khang Nguyen Thanh's answer which follows this one is similar but looks algebraically less messy.)
We are looking for the integral points on the line that passes through ( 0 , 0 ) and ( m , n ) whose equation is y = m − 0 n − 0 x ⟹ y = g cd ( m , n ) m some integer x
(Note above: Reducing a fraction to lowest terms involves dividing the numerator and denominator by the greatest common divisor of both; the numerator isn't important here, since we know it's an integer.)
Thus, x must be a multiple of g cd ( m , n ) m in order to get integer values for y . That is x = g cd ( m , n ) m k and we know that 0 ≤ x ≤ m , so 0 ≤ g cd ( m , n ) m k ≤ m ⟹ 0 ≤ k ≤ g cd ( m , n ) Therefore g cd ( m , n ) + 1 points of the grid lie on the big triangle's hypotenuse.
(Note that the +1 is because we have 0 to g cd ( m , n ) inclusively, so if we tried to say the answer was just g cd ( m , n ) we would omit the point at ( 0 , 0 ) . )
Your solution has a typo it is (1200,1000).
I solved the problem of the same way :)
Solved it the same way!
General result:
With m , n are positive integers, the number dots from the grid lie on the segment between ( 0 , 0 ) and ( m , n ) is g cd ( m , n ) + 1 .
Prove :
Let ( x , y ) is a point lies on the segment between ( 0 , 0 and ( m , n ) if and only if: 0 ≤ x ≤ m , 0 ≤ y ≤ n and x − 0 y − 0 = m − 0 n − 0 Let d = g cd ( m , n ) and m = d m 1 , n = d n 1 .
We have: x y = m 1 n 1 .
Because m 1 n 1 is irreducible, x = k m 1 and y = k n 1 , where k is a integer.
Since 0 ≤ x ≤ m , 0 ≤ y ≤ n so 0 ≤ k ≤ d , there are d + 1 possible values of k .
So the number dots from the grid lie on the segment between ( 0 , 0 and ( m , n ) is d + 1 or g cd ( m , n ) + 1 .
In this problem, the answer is g cd ( 1 0 0 0 , 1 2 0 0 ) + 1 = 2 0 1 .
The "suppose that" at the beginning of your argument is inappropriate.
By creating a line through (0,0) and (1200,1000) we get an equation of y=
1
2
0
0
1
0
0
0
x or y=
6
5
x. Since the slope is reduced to
6
5
then we can locate a new red dot every time (starting at the origin) we move 6 units to the right (x value) and 5 units up (y-value). Since we find a red dot every 6 units to the right we can take the total units to the right which is 1200 and divide that by 6 or
6
1
2
0
0
= 200 and then add the red dot at the origin which gives us 200 + 1 or 201 red dots.
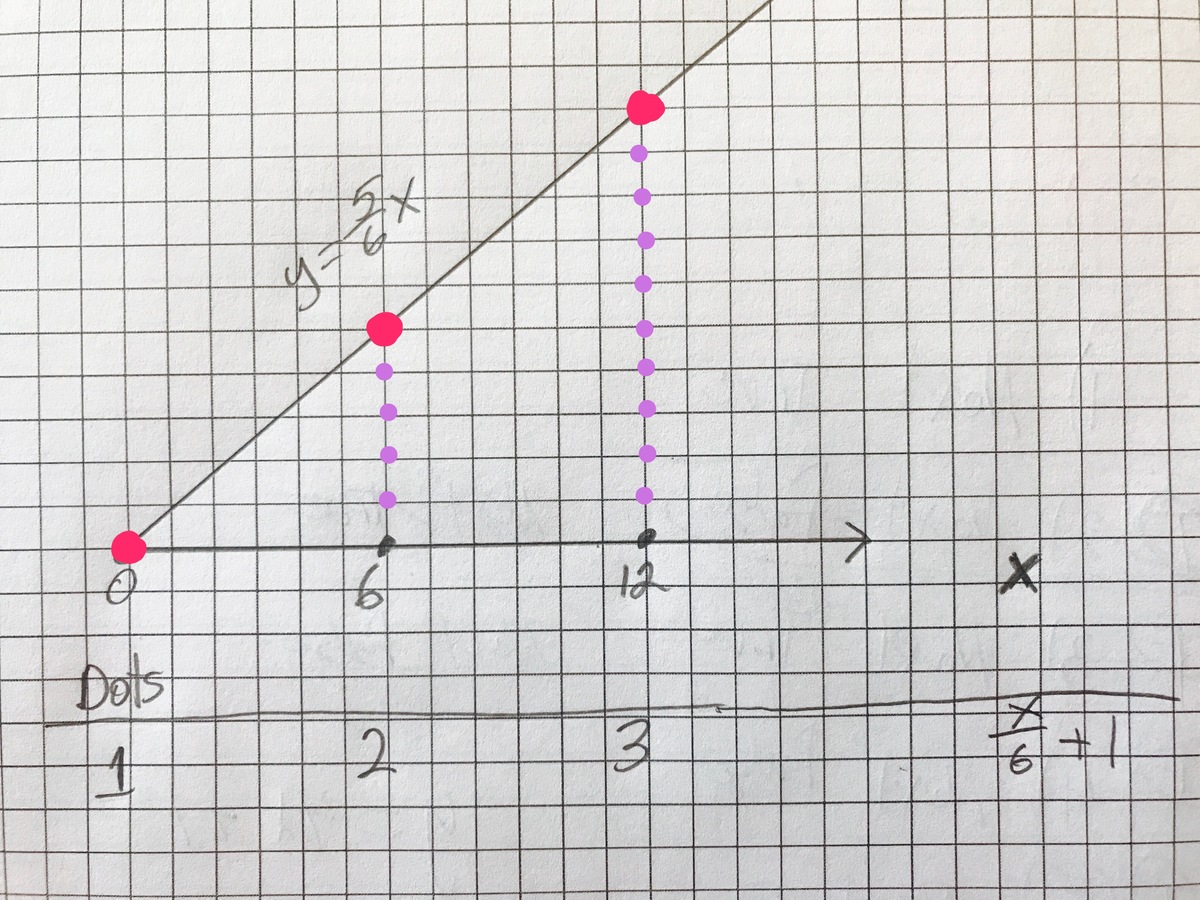
That's how I thought about it! The LCD of 1200,1000 is 6,5 so 6,5 200 times over again is 1200,1000 (6 200=1200,5 200=1000) plus the red dot at 0,0 (point of origin) gives 201.
I'm so confused! I thought it was 301, They said this triangle, so there's already a red dot at (4,4) and (8,6) so did you leave it out? This triangle's slope is 6/8. The triangle they've asked about has a slope of 5/6 - which is a different triangle, so why didn't they say that if another triangle which has a slope of 5/6 and vertices at (0,0), (1200,1000) and (1200,0), and has red dots spaced .... oh hang on, I've got it, it is a different triangle altogether. Ah, now it all makes sense. Oh now you're answer also makes sense, but what on earth is everyone else on about? They used the definite article instead of indefinite, the instead of a, in the second sentence and totally destroyed my brain! Phew.
Be careful M&R - the precision of the English has been commented on more than once. This is by far the easiest method - it requires no prior knowledge - just a bit of common sense
An equation for the hypotenuse in lowest terms is 6y = 5x using elementary linear algebra.
For (x,y) to have integral coordinates ("on the grid"), 5x must be divisible by 6, and 6y must be divisible by 5. This only occurs when x = 6k for k = 0, 1, .... because the coefficients in lowest terms are relatively prime.
Points y will thus be on the hypotenuse and the grid when x = 6k AND 0 ≤ 6k ≤ 1200.
That would be k = 0, 1, ..., 200 or 201 points on the grid.
Within the triangle with points (0,0), (1200,0), and (1200,1000) (or any generic right triangle), it is possible to draw an infinite number of similar right triangles by drawing an altitude from an arbitrary point of the base of the triangle to the hypotenuse. Since all the grid points are at whole number coordinates, we need to find how many of these triangles have whole number length sides. We can do this by finding the ratio of side lengths of the original triangle, which is 6/5 when simplified if you start with the long side (not the hypotenuse) over the short side, and then seeing which multiples of this value produce whole numbers. Since the denominator of the fraction is 5, clearly 5 or any multiple of 5 will make this a whole number. Remembering that the 5 represents the short side of the triangle and the length of that side in the original triangle is 1000 units, we divide 1000 by 5 to get 200. However, this does not account for one of the end points of the triangle (because we cannot draw a similar triangle with side length 0) so we must add 1. Therefore, the answer is 201.
The line crosses a dot for every multiple of the reduced form of the slope.
So if our slope is 1 2 0 0 1 0 0 0 , the reduced form is 6 5 .
6 5 goes into 1 2 0 0 1 0 0 0 200 times.
Including the dot at (0,0), we see that there are 200+1 = 201 dots crossed.
first simplified the the fraction 1 0 0 0 1 2 0 0 to 5 6 then I put it as 2 points in the plane, and so at point (0,0) there would be 1 red point, at (6,5) 2 and so on, then what matters is that as you add 6 to the x's you get a new point, so you get a sequence of 0,6,12,18,24 and you get the equation 6(n-1), n would be the nth term which turns out to be the number of red points as well, and 6(n-1)=1200 would give us that n=201 which is 201 red points as well....
For a moment just focus of the given diagram.
In the given triangle we can see the slope is
m =
8
6
i.e. m =
4
3
now since it passes through the origin the equation of hypontenuse is given my
y =
4
3
x + 0
So for y to have integral values, x must a mulitple of 4.
Thus, for a triangle with base of 8 units there are 3 mulitiples (0,4,8) hence 3 red dots. i.e.
4
8
+1 = 3
Now comming to the Question, For the given question, m = 1 2 0 0 1 0 0 0 i.e. m = 6 5 So, for a triangle with base of 1200 units there are 2 0 1 .
The number of points that intersect is equal to the number of points that are integers on the linear equation 6 5 x = y Thus, we want the number of value of x from 0 to 1200 (both inclusive) that results in a integer solution, OR simply asking: How many numbers are divisible by 6 from 0 to 1200? The formula for that would be: f l o o r ( 6 1 2 0 0 − 0 ) + 1 Which is, of course, 201
The right triangle with vertices at (0, 0), (1200, 0) and (1200, 1000) is a 200 times scale copy of a right triangle with vertices at (0, 0), (6, 0) and (6, 5). The hypotenuse of the small right triangle touches a grid point at (0, 0) and (6,5). There are 200 copies of that small right triangle aligned along the hypotenuse of the large copy of the right triangle. The hypotenuse vertices of each of those small triangles touches a grid point (i.e. at (6, 5) and (12, 10) for the 2nd copy). Each copy adds one grid point touched to the total. Therefore, there are 200 grid point vertices on that hypotenuse (i.e. at (6, 5) (12, 10) (18, 15) and so on up (1200, 1000) ) and there is the original vertex at (0, 0) for a total of 201 points.
Y=mx+c
0=0(m)+c
c=0
Also
1200=1000(m)+0
m=1000/1200=5/6
Y=(5/6)x
When x is any multiple of 6 , Y will be a whole number .
Using AP
a(n) = 1200
a = 0
d=6
1200= 0 + (n-1)6
n-1 = 1200/6=200
n=201
5x=6y so y =0,5,10...2000 therefore (2000-0)/5 +1 =201
Question is how many dots are on the line (0,0) to (1200,1000) or(A,B)
Let C is greatest common denominator of A and B then the number of dots will be C +1 Let check with (8,6) GCD is 2 then number of dots will be 2+1 = 3 Let calculate with (1200,1000), GCD will be 200 then number of dots will be 200 +1 =201
The question can be deduced to find the number points with integer coordinates that lie on the line (Y-0)=(1000-0)/(1200-0) (X-0) =>Y=(5/6) X since we know that Y,X are integers so for Y to be an integer x should be a multiple of 6, we also know that 6<=X<=1200 we have to find the number of X's in the range which are integers and a multiple of 6 which can be calculated as number of terms of an AP whose common difference is 6 and first term is 6 and last term is 1200 n(number of terms)={(1200-6)/6}+1=200 now by default one point is (0,0) adding that to the whole list, the total number of integral solutions will be 201.
This is going to be pretty informal, but here goes: I noticed that for the 6-8-10 triangle, there was one more than the number of 3-4-5 triangles that fit in it. So for he 1200-1000 triangle, I found that the hypotenuse was 200√61, so the smallest version would be a 6-5-√61 triangle and there would be 200 of them that fit in the large one. 200 + 1 = 201
I Just solve it with programing by : python and this is my Code
The slope of the line described is 6/5, the run is 1000, 1000/5= 200 and then add one for the initial red dot = 201
The triangle with coordinates ( 0 , 0 ) , ( 1 2 0 0 , 0 ) , ( 1 2 0 0 , 1 0 0 0 ) is "genereted" by the triangle ( 0 , 0 ) , ( 6 , 0 ) , ( 6 , 5 ) just scaled by a factor of 200 so the total number is 201 (we add the point 0,0)
Simplifying the ratio 1000:1200 gives 5:6. 1000/5 = 200 so from the initial point you will have 200 points, add on the starting point gives 201 points 😁
The condition for a point on the hypotenuse to coincide with the grid is that the distance from the origin to the point in the horizontal and vertical directions (let's call them x and y) are both integers.
y is on the hypotenuse if y=H/W*x, where H and W is the height and the width of the triangle. Reduce H/W until no common factors remain and call the result h/w. Then y is an integer if x = w. The number of points on the hypotenuse that coincide with the grid are thus W/w+1.
In the present case, 1000/1200=5/6. So the number of points on the hypotenuse is 1200/6+1=201.
Relevant wiki: Linear Diophantine Equations
We are looking for the integral points on the line that passes through ( 0 , 0 ) and ( 1 2 0 0 , 1 0 0 0 ) whose equation is y = 1 2 0 0 − 0 1 0 0 0 − 0 x ⟹ y = 6 5 x Thus, x must be a multiple of 6 in order to getting integer values for y . That is x = 6 k and we know that 0 ≤ x ≤ 1 2 0 0 , so 0 ≤ 6 k ≤ 1 2 0 0 ⟹ 0 ≤ k ≤ 2 0 0 Therefore 2 0 1 points of the grid lie on the big triangle's hypotenuse.