17 of 100: Sorting Numbers
If this Venn diagram is filled with all positive integers , how many of the regions marked with a letter will be empty?
Think carefully about each region! Make a justification if you believe a region is empty.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
While it doesn't have to be lengthy, you still need a justification that C is empty.
Nitpick: 3 is not in A and 2 is not in E. Along those lines, multiples of 6 are in D (where you have them) and not in A. Also 2 and 3 are not in E.
Remember that these letters only refer to subsets, not the entire sets themselves. So, by definition, E only contains the primes that are not divisible by 2 or 3, for example.
Log in to reply
Yes, that's true. Alphabets are used in the question to represent disjoint 'regions' not sets so that no two regions can share the same numbers. The solution need edits.
That was a serious mistake by my side. Sorry for that... Thanks for letting me know about it. I've edited the solution.
And 2 5 ∈ H .......
There is no talk about the set H.
H can contain a number who is only divisible by a prime number (and by himself)
I don't think there was any set H when I wrote the solution. I wrote this solution a week ago. Maybe they added it later. Anyway, thanks for letting me know about it... I'll soon edit my solution... Thanks...
Incorrect. B should not have a set. There are no numbers both divisible by 3 and prime...
Log in to reply
3 is a prime number, and is divisible by 3 since 3/3 = 1.
To show that a region represented by a particular letter is not empty, all we have to do is list a single element of that set.
9 ∈ A (divisible by 3, odd, not prime)
3 ∈ B (divisible by 3, odd, prime)
6 ∈ D (divisible by 3, even, not prime)
5 ∈ E (not divisible by 3, odd, prime)
2 ∈ F (not divisible by 3, even, prime)
4 ∈ G (not divisible by 3, even, not prime)
2 5 ∈ H (not divisible by 3, odd, not prime).
Region C is the only one left. For it not to be empty, there would have to be a prime number divisible by both 2 and 3 . But a prime number, by definition, may only be divisible by 1 and by itself, so it may not be divisible by two numbers different from 1 and from each other. The set C is therefore empty.
•
A
={
3,6,9,12
...} (Multiple of 3)
•
B
={
3
} (Prime and multiple of 3)
•
C
={}. [
the set C is the only null set as there is no positive integer which is prime and also divisible by {(3×2)=6}
]
•
D
={
6,12,18
...} (Multiple of 6)
•
E
={
2,3,5,7,11,13,17
...} (Prime)
•
F
={
2
}. (Prime and even)
•
G
={
2,4,6,8,10
...}. (Even)
•
H
={
1,25,35,49,55,65
,...}. (Except prime and multiple of 3 and 2) .
So, the answer is
1
.
H also contains the number one!
Note that the sets are drawn to be disjoint, so no number can be in both A and B, for example.
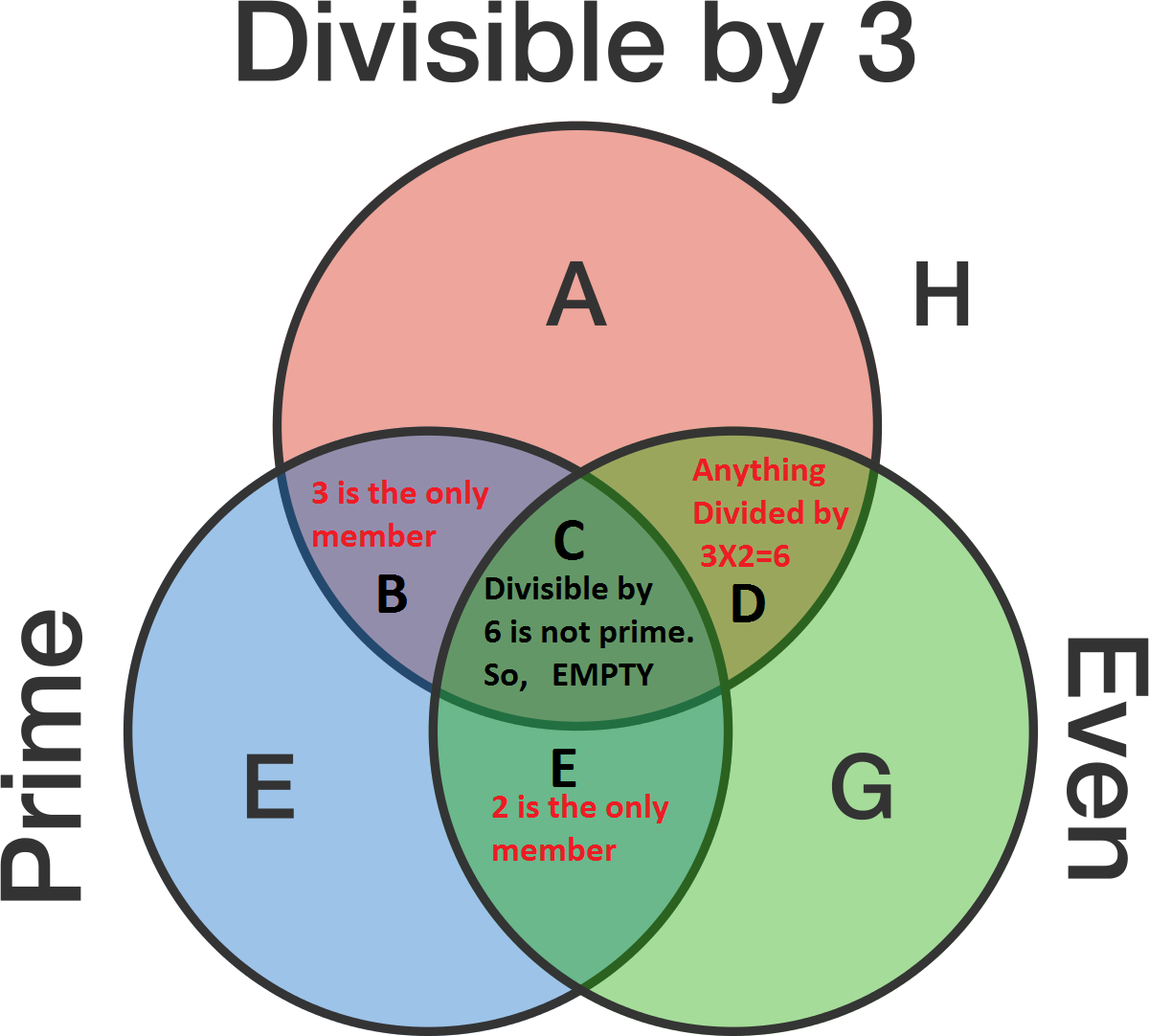 BC
= Prime number which is DIvisible by 3. Only 3 is a prime number and divisible by 3. Other multiples of 3 like 6, 9, 12.... are not prime-number.
So,
3 is the only member in BC region.
BC
= Prime number which is DIvisible by 3. Only 3 is a prime number and divisible by 3. Other multiples of 3 like 6, 9, 12.... are not prime-number.
So,
3 is the only member in BC region.
CF = Prime number which is an even number. Only 2 is the single EVEN prime number. Other even numbers like 4, 6, 8, 10, 12.... are not prime-number. So, 2 is the unique member in CF region.
CD = Even number which is Divisible by 3. So, the numbers will be divisible by 2 ( for the even number) and 3 = 2X3 = 6. So, the members will be 6, 12, 18, 24.... etc
C = This Region has to satisfy all conditions from BC CF CD regions. There is no common element among BC=3, CF=2, CD= 6, 12, 18.... So, C region will be the empty one.
The number of Empty Region is 1.
Only set C is empty as it's not possible for being prime and having 2 and 3 as it's factors,as it itself contradicts the definition of a prime.
The definition of prime is that it is only divisible by 1 and itself. It can be divisible by 3 or by 2 but not both.
Just start looking at the positive integers, and before you arrive at ten you'll have all categories filled-- except for one, 1 .
1 2 3 4 5 6 7 8 9 ⋮ H F B G E D E G A ⋮ This is the only even prime number. This is the only prime number divisible by two. All prime numbers from here on go here. All multiples of 6 go here. Together with all odd multiple of 3 from here on.
We only have nothing yet for category C . To prove it is actually empty, consider that if a number is even and divisible by 3, it has at least the prime factors 2 and 3 . It is therefore not a prime number.
Why there belongs 2 E set in your answer?
Your question is not entirely clear.
If you mean "Why did you place two numbers in set E ," the answer is that both 5 and 7 are prime numbers that are not even and not divisible by 2.
If you mean "Why does 2 belong to set F ," the answer is that 2 is even, and since its only factors are 1 and itself it is a prime number.
There are plenty of prime numbers, even numbers, and numbers divisible by three. There is one even prime number, which is two. A prime number divisible by three is three. An even number divisible by three is six. Even Prime numbers divisible by three would have to be empty because it could only be multiples of six, which are not prime. The number one is not prime, even, or divisible by three
I suppose that the answers all have to be integers correct? Because I would argue that 2 would fill both C and F. It didn't specify that the results had to be integers just that values you choose have to be integers.
But two is not divisible by 3.
Log in to reply
Yes it is 2/3 or .66666 repeating. You meant to say it's not a multiple of 3.
Log in to reply
Saying two isn't a multiple of three is the same as saying two isn't divisible by three.
"An integer n is divisible by another integer m if m is a divisor of n; this implies dividing n by m leaves no remainder." https://en.wikipedia.org/wiki/Divisor
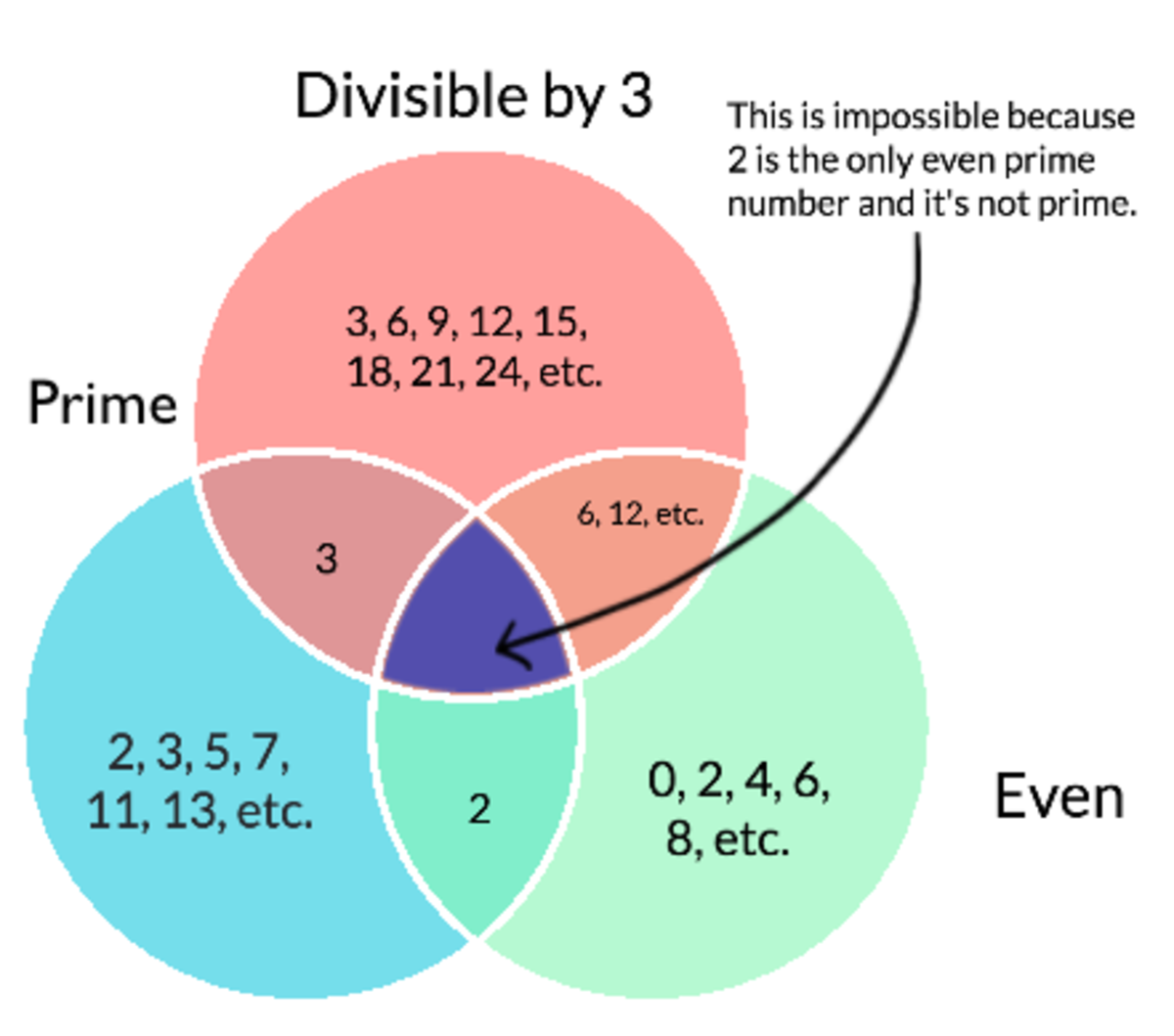
As we can clearly see that only set C is empty, the answer is 1.