23 of 100: Speedy Pie Baking
It takes 5 cooks 5 hours to bake 5 pies. Assuming no change of rate, how many hours will it take 10 cooks to bake 10 pies?
They're strawberry rhubarb pies.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
26 solutions
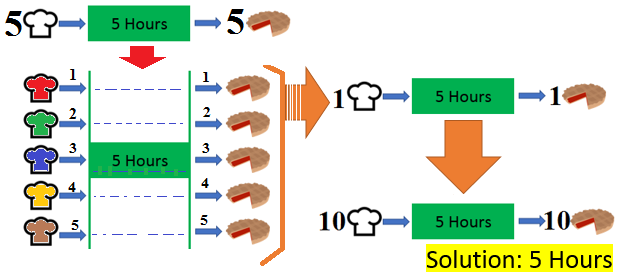
I solved it the same way
A more formal solution (which is absolutely unnecessary here, but great when things get harder):
In situations like this, the output (the pies) is directly proportional to the input (cooks and hours). Thus P ∝ c ⋅ h . This means that c 2 ⋅ h 2 P 2 = c 1 ⋅ h 1 P 1 . Cross-multiply: P 2 ⋅ c 1 ⋅ h 1 = P 1 ⋅ c 2 ⋅ h 2 . Solve for the unknown h 2 : h 2 = P 1 ⋅ c 2 P 2 ⋅ c 1 ⋅ h 1 = P 1 P 2 ⋅ c 2 c 1 ⋅ h 1 . Plug in what we know: h 2 = 5 1 0 ⋅ 1 0 5 ⋅ 5 = 2 ⋅ 2 1 ⋅ 5 = 5 .
These formulas look a bit like working with the generalized ideal gas law, P ⋅ V T = const. So let's translate the problem of the cooks to this physics context:
If it takes a pressure of 5 atm to fit gas at 500 K in a 50-liter container,
how much pressure does it take to fit that same gas at 1000 K in a 100-liter container?
Now it is suddenly a lot more difficult to do it intuitively, unless you have really internalized the behavior of ideal gases. The math is perfectly analogous to the solution above.
The question asks "how many hours will it take 10 cooks to bake 10 pies" which could be viewed as two groups each of five cooks working on five pies at the same time(the two groups are working separately at the same time). And this would certainly take the same time it takes "5 cooks to bake 5 pies". So the answer is 5.
Yes... I think your answer is more inductive and easier to understand. That is also the way I approached this question.
I'm not clear on what "no change of rate" specifically applies to.Pie:Bakers? Pie:Hours? Looking at it in process terms (I used to be an industrial software guy) my question is "what makes it take 5 bakers 5 hours?" In other words, does it take 5 hours because the baker works on a cake for 5 minutes and then bakes it for 4:55, or does it take a baker 4 hours and it bakes for 1 hour? How many ovens are available? There is actually not enough information to answer the question.
But since we start out with 5 bakers taking 5 hours (and not 1 baker taking 1 hour) and my job isn't on the line, I can assume there are no significant opportunities to optimize parallel tasks or otherwise synergize a larger team, so I can assume that it will still take the first 5 bakers 5 hours to make their pies. This is consistent with "no change of rate." The "no change of rate" also suggests that there won't be a bottleneck about the ovens. So I answered "5 hours" on the theory that we have 2 teams of 5 bakers working in parallel.
In the real world, I'd say "10 hours" until somebody clarified that there is enough oven space (and other equipment) for 10 simultaneous cakes. And my experience tells me that my 10 hours would be underestimating unless the bakers were serious, experienced professionals and not interfering with each other. In the real world, with people I have worked with, and realizing 5 hours is more than half a work day, the preliminary answer is 2 days. Then we multiply by 2 and move up a time unit, because estimates are always wrong. So the correct answer is 4 weeks.
As a math teacher in training, I am becoming a real stickler for making "real-world" problems real. When a student is required to leave his or her life-experience at the gate (for example, problems that assume a pizza place sells a 1/8 slice of a pizza for 1/8 the price of a full pizza) we teach students that math (at least the math we are teaching them) is not applicable to real life.
Yeah - though I defend not-perfect English on many questions - this really doesn't make sense because any cooking has prep time and cooking (baking) time - my first thought was also 'oven space', before we even start on your other comments.
Log in to reply
I hope I'm not being too picky on the English in questions. I'm more concerned with logic where bringing reality into the situation completely messes up the math. Things where you have to pretend you don't know about the subject in order to get the right answer.
I'm not concerned with minor inaccuracy either. Math questions about cars that ignore wind resistance generally aren't a problem. But prep time and baking time and oven space can be. The point of this kind of problem is to apply math to life. But that only works when the student can also apply math to life.
In this context, I'm just being picky. You (I assume) and I already apply math to life by habit. But for my students, who still ask "why do I have to l do this?" I think it is important to let their life inform their math.
One of the joys of teaching spread sheeting was that the 'what's the point of learning this?' brigade almost invariably lit up with delight and threw themselves completely into it (oh - it wasn't you being picky wrt English - that referred to other people in other questions) I also used to fling in Q's like this, where I would hope to be told the info didn't make sense, or Q's where the info was incomplete, as I taught GAT kids, & I warned them, one day they might be Finance directors and would need to stand up to their Chair and say......
Log in to reply
Love to hear "Mr. Huber, that doesn't make sense!"
An easy solution can be as follows:
| Cooks | Pies | Hours |
| 5 | 5 | 5 |
| 10 | 10 | X |
⟹ X = 5 × 1 0 5 × 1 0 × 5 = 5
Then the answer is 5 hours.
It takes 5 cooks 5 hours to bake 5 pies. When they have 10 cooks and 10 pies, they have twice as many pies to bake, but they have twice as many people, so the time it takes should be the same. So, it takes 5 hours for 10 cooks to cook 10 pies. But the thing that's worrying me at the moment is the one slice missing from the pie above. Could it be this one?

We want double the amount of pies, but we also have double the amount of cooks available. The time is the same.
M1=5
M2=10
P1=5
P2=10
H1=5
H2=x
M1 H1 P2=M2 H2 P1
5 * 5 * 10= 10 * x *5
x= 1 0 ∗ 5 5 ∗ 5 ∗ 1 0
Therefore x=5 Hours
You can just think of this as the 10 cooks being 2 lots of 5 cooks, and so put each of the 2 groups of 5 cooks into separate kitchens. And then for each kitchen you would have 5 cooks baking 5 pies, which you are told in the question takes them 5 hours. And you are also told that the rate of baking does not change. So the answer will be the same as before - 5 hours. Regards, David
one cook bakes one pie in one hour is the rate. therefore 10 cooks take 1 hour to bake 10 pies
The solution appears that to be 5 hours, but the problem with this is not really accurate because of other resources needed. We all know that no pie bakes for 5 hours, nor does it take 4 hours to prep the ingredients to bake one pie, therefore it is not unreasonable to believe that the cooks must be sharing some resources, which results in the five cooks not completing the five pies in about an hour. Assuming it takes on average .5 hour for the pie to bake, and .5 hours for a cook to prepare the pie to go into the oven, then it would mean each cook was working sequentially on baking a pie. (i.e. the first cook made his pie and baked it in the oven that held one pie, cleaning the work area and tools while his pie baked), After the hour was up, the next cook now had resources available and cooked at the same rate. After 5 hours, 5 pies would be completed.
Using this knowledge, it would take 10 hours for 10 cooks to make 10 pies, each working at the same rate (using the prep area and oven for 1 hour). We made some assumptions here, but since the 5 cooks could not complete the 5 pies in less than 5 hours, there must be a limit on resources, and therefore it could not take less time, eliminating answers 1 and 2. If more than one cook could prep and bake a pie at once, then the five cooks could have completed their pies in 3 hours or less. Since it took them 5 hours, the only conclusion is that all cooks must work sequentially and the only answer left is 10 hours.
| Cooks | Hours | Pies | |
| Row 1 | 5 | 5 | 5 |
| Row 2 | 5 | 10 | 10 |
| Row 3 | 10 | 5 | 10 |
5 cooks, 5 hours, 5 pies (row 1) means those same 5 cooks would need 10 hours to make 10 pies (row 2). Now, if you double the number of cooks, the time is cut in half (row 3). So, 10 cooks need 5 hours to make 10 pies.
see, it takes 5 cooks to cook 5 pies in 5 hours. and when 10 cooks will cook then let us divide them in 2 teams of 5 cooks.
now at the same time Team 1(consisting of 5 cooks) :- cooking 5 pies in 5 hours {at the same time} Team 2(consisting of 5 cooks):- cooking 5 pies in that same 5 hours
Therefore finally we have tow teams of total 10 cooks who have cooked 10 pies in 5 hour.
5 cooks, 5 hours, 5 pies
5 cooks, 10 hours, 10 pies
5 x 2, 10 / 2, 10/1
10 cooks, 5 hours, 10 pies
Using inverse ratios, we can tell that double the amount of people is half the amount of hours. Hence, the answer is 5 hours
we can write this as a ratio 5:5:5 we double the cooks, we half the time or double the pies, so we either have 10 : 2.5 : 5 or we could have 10 : 5 : 10 working off of 10 : 2.5 : 5, we then double pies AND double the time getting 10 : 5 : 10, or working off of 10 : 5 : 10 we already have the answer :P
5 cooks 5 hrs to make 5 pies [ here pies are result ] we can say that 5 x 5 = 25 man hours were needed for 5 pies
so for 10 pies it will obviously take 25 x 2 = 50 man hours
but in question it is given that there are 10 cooks for this job so only variable that can be changed is time.
So time needed for making 10 pies = 1 0 5 0 = 5 hrs
5 cooks: 1 pie per hour, so double the cooks is double the speed, 10 cooks: 2 pies per hour.
One cannot hurry a baking pie. (Note that the question is only about the baking process, and not about any other aspects of pie preparation).
One pie, 5 pies, 10, or a thousand, each has to bake for 5 hours. If you bake them all at once, they all will be done in five hours.
If you had another team of these 5 cooks, they'd also take 5 hours to bake 5 pies.
Taken all together, the 10 cooks (in two teams of 5) need 5 hours to bake 10 pies.
This is another example of the same kind of question. Explaining the logic to 7th graders isn't easy: if it takes a hen and a half a day and a half to lay an egg and a half, how many eggs will 24 hens lay in 24 days?
5 cooks - 5 hours - 5 pies, the same 5 cooks then bake 10 pies in 10 hours, and with double the cooks, half the time, so 5 hours.
It would take each cook 5 hours to make 1 pie, so therefore it will still take 5 hours for 10 cooks to make each a pie.
-
Because it takes 5 cooks 5 hours to bake 5 pies, we can then assume that it will take 1 cook 5 hours to bake 1 pie.
-
Explanation Why: Dividing the number of cooks by 5 does not reduce the time. Instead you divide amount made, the pies by 5, to get 1 cook needs 5 hours to bake 1 pie.
-
Thus, for 10 cooks to bake 10 pies, we will still need 5 hours. (Same logic, multiplying the number of cooks by 10 (from 1) also multiplies the amount of pies made ,1, by 10, so 5 hours is still our answer.)
5 cook make 5 pies in 5 hours
So each cook will make 1 pie in 5 hour
necessarily 10 cook will made 10 pies in 5 hour
The general idea of rate here is that of labor hours per item produced. 5 cooks each working 5 hours is 25 labor hours. That works out to be 5 labor hours per pie. That means that to make 10 pies 50 labor hours are required, and dividing this by 10 cooks gives 5 hours. This method makes the reasoning straightforward even if the numbers are not as even. I can't stand these problems, though! Maybe it is because as a former baker I know how unrealistic they are!
Since each cook is baking his/her own pie, it takes 1 cook 5 hours to bake 1 pie.
Therefore, using this known ratio, if 10 cooks did his/her pie, it would take them 5 hours to bake 10 pies.
This one kind of tricks you, because at first the answer seems obvious: 10. But this is not the case: since he ratio is the same, the time is also the same. So it will take the same amount of time, namely 5 hours.
This question is a classic.