This is an efficient way to find $\color{#D61F06}X$ for any given number $a$ . Here we find $\color{#D61F06}X$ for $a=42$ .

Its easy to see that $\color{#D61F06}X$ is in the form $10^{n_1}+10^{n_2}+...+10^{n_k}$ , where $n_1>n_2>...>n_k \ge 0$ . We need $10^{n_1}+10^{n_2}+...+10^{n_k} \equiv 0 \pmod{42}$ Find remainders of powers of $10$ divided by $42$ . We want to see when a sum of these remainders becomes $0$ mod $42$ .

$10^0 \equiv 1 \pmod{42} \\ 10^1 \equiv {\color{#D61F06}10} \pmod{42} \\ 10^2 \equiv 100 \equiv 16 \pmod{42} \\ 10^3 \equiv 10 \times 100 \equiv 10 \times 16 \equiv 160 \equiv {\color{#D61F06}34} \pmod{42} \\ 10^4 \equiv 10 \times 10^3 \equiv 10 \times 34 \equiv 340 \equiv 4 \pmod{42} \\ 10^5 \equiv 10 \times 10^4 \equiv 10 \times 4 \equiv {\color{#D61F06}40} \pmod{42}$

Thus the smallest number is $10^5+10^3+10=\color{#D61F06}101010$ , which is $40+34+10 \equiv 84 \equiv 0$ mod $42$ .

Note : This answer is long, but I hope to fully explain the solution to the problem. If something is unclear or confusing, please comment it below so I can fix it. Thanks! [0]

Solution

First of all, for a number to be divisible by a composite divisor (42 is composite), it must be divisible by its highest power of its prime factors. [1] Since $42=2^1\cdot3^1\cdot7^1$ , our base 10 number composed of only 1's and 0's must be divisible by 2, 3, and 7. We will build our number by looking at each of these factors in turn.

As an absolute truth, any positive real number with more digits than another is greater than the other number. [2] Because we are looking for the smallest number that satisfies the conditions given, it makes sense to start with numbers that have a small number of digits and work our way up.

The factor 2 is trivial. For any number to be even (divisible by 2), the last digit must also be even. [3] Because we may only choose from 1 and 0 for the digits of our number and 1 is odd, the last digit must be 0.

Divisibility by 3 is also rather easy. To be divisible by 3, the sum of the digits of the number must also be divisible by 3. [3] Since 0 as a digit does not add to the sum, we know the number of 1's has to be a multiple of 3. There can't be zero 1's (that would give us just 0, and 0 is not positive), so let's assume the next smallest possibility, 3 1's, and work from there.

The factor 7 is the hardest. We can compute the residue (a.k.a. remainder) modulo 7 of powers of 10 using modular arithmetic: $10^1\equiv3,10^2\equiv2,10^3\equiv6,10^4\equiv4,10^5\equiv5\textrm{ }\ldots\textrm{ }(\textrm{mod }7)$ . [4] This is useful as a number composed of only 1's and 0's is just a sum of some of these powers. [5] Since we have 3 1's in our number (for now), we must choose 3 powers of 10 to be added up to form our number. To make the number divisible by 7, according to modular arithmetic, the sum of the residues of the 3 powers must also be a multiple of 7. [6] So all we have to do is to choose 3 numbers from the list that add up to 7, 14, etc., trying to stick to the left of list to minimize the final sum.

We see that $3+6+5=14$ from the list above after a small amount of trial-and-error. Choosing the smallest powers of 10, this corresponds to $10^1+10^3+10^5=101010$ .

Notes and References

[0] This is also my first time using LaTeX, so please tell me if something breaks.

[1] For example, if the divisor were $72=2^3\cdot3^2$ , the dividend must be divisible by both $2^3=8$ and $3^2=9$ . See this Wikipedia page for more.

[2] More formally, $\lfloor\log_{10}a\rfloor >\lfloor\log_{10}b\rfloor\Rightarrow a>b$ .

[3] See Brilliant Wiki on Divisibility Rules for a review.

[4] Inspiration for this strategy came from this Wikipedia page (third paragraph) because I was too dumb to come up with the strategy myself. To be honest, Brilliant's wiki was not too helpful for this part of the solution. This can also be calculated in one's head using these rules here .

[5] As an example, $10110=1\cdot10^4+0\cdot10^3+1\cdot10^2+1\cdot10^1+0\cdot10^0$ .

[6] Somewhat comes from the third rule here .

1) 42 is divisible by 2, X must be divisible by 2.

So, the last digit must be 0.

2) 42 is divisible by 3, X must be divisible by 3.

So, sum of the digits of X must be divisible by 3.

3) The last digit is 0, X is divisible by 5 too. So X must be greater or equal to 42*5 or 210. This also requires for X to have more than 3 digits.

4) 42 is divisible by 7. X must be divisible by 7. From divisibility rules we know a number is divisible by 7 if subtracting twice the last digit of N from the remaining digits gives a multiple of 7. (e.g. 658 is divisible by 7 because 65-2*8=49, which is a multiple of 7)

101010 is the first number that satisfies all of these conditions

If it's divisible by 42 it must be divisible by 2 and 3 and 7. I started with only 2 and 3. Because X is divisible by 2 it must end with a 0. And because X is divisble by 3 there must by at least three 1's in X. Then I did some trying: 1110 is not divisble by 7. 10110 is not divisible by 7. 11010 is not divisile by 7. 11100 is not divisible by 7. 100110 is not divisible by 7. 101010 is divisble by 7. The answer is 101010.

Since positive number X is divisible by 42 , by converting 42 into base 2 , we will get 101010 in base 2 is equal to 42 in base 10. Thus, 101010 is the smallest number that is by 42, and is composed of only 1s and 0s only.

I took a slightly different approach to the other ones already given, so I though I'd write it up.

Since the prime factors of 42 are 2,3 and 7 what ever number we find has to be divisible by all three of these numbers at the same time. I used the same divisibility rules as everyone. The number had to end in 0 so it would be divisible by 2, and the number of 1s needs to be a multiple of 3 to be divisible by 3.

My method for finding the number consisted of trying to find the number that when multiplied by 7 gave a number in the specified format (only consisting of 1s and 0s) and that fulfilled the rules for divisibility by 2 and 3 written above. Yielding a number divisible by 42.

So basically I started by choosing digits of the multiplier of the number 7 knowing it started with a 0. The next number should give 1 when multiplied by 7, since we don't want a bunch of 0 at the start (we are looking for the smallest number divisible by 42 after all), so the only choice is 3. Now we have $30 * 7 = (2)10$ (the 2 is the carry since we're not done yet). This is where the trial and error part of the solution starts, since we need to choose the next number carefully.

The key part of the solution is to realize that if our current carry is 2 or 3 we can write down 4 as the next digit of the multiple, which puts us in a good spot, since it gives us a carry of 3 again. So we can keep on adding 4 to the multiplier, which adds 1 to the left of our solution and gives us carry 3. Carry 3 is great since we can, at the appropriate time, choose 1 as the next digit which adds 10 to the end of the solution, ending the process.

Since we have $30*7 = (2)10$ we add the 4 straight away and get $430*7 = (3)010$ . Following this logic the whole process goes as such:

         0*7 =       0
        30*7 =   (2)10
       430*7 =  (3)010
      4430*7 = (3)1010
     14430*7 =  101010

The interesting part of this solution is that when we get to the part where we add 4s to the multiplier we can add as many as we want, and as long as we pay attention to the number of 1s in the solution (so we maintain divisibility with 3), we will still have a number divisible by 42. For example, the following numbers are also divisible by 42: 101111010, 101111111010, 101111111111010, 101111111111111010 ...

What about a C++ solution? :D

"#include <iostream>

using namespace std;

int x=0,f=0,s=0,m;

int main() {

while (f==0){

x+=42; m=x; s=0;

while (s<2 && m!=0){

s=m%10;

m/=10;

}

if (s<2){cout<<x; f=1;}

}

return 0;

} "

Placing the code between the quotation marks in a C++ playground yields the solution in a few seconds.

Maybe someone can help me with the reason why this works. The answer to this puzzle is 101010. 42 in binary is 101010.

The smallest number made up of 1's and 0's that is divisible by X is the binary version of X.

$42$ can be split into its prime factors, $2 \times 3 \times 7$ , so we can deduce some facts about the digits in X using the divisibility rules.

1. X must be even and hence must end with a zero.

2. X must contain at least 3 digits that are 1 in order to be divisible by 3. If we can't find a solution with this constraint then we need to look at numbers with 6 digits that are equal to 1 (and then 9 etc.)

3. There is no advantage to having an extra divisor of 10 in the solution, so X must end with the digits 10.

4. The 2nd divisibility rule for the digit 7, contains the sequence $1, 3, 2, 6, 4, 5$ . Since X contains only zeros and ones, we just need to find 3 digits in this sequence that add up to a multiple of 7. Starting from the least significant digit, put a 1 in our number X for the digits in the sequence that we use, and a zero for those we don't. We have already deduced that X ends in 10 so the first digit in the above sequence that will be used is 3.

$3 + 6 + 5$ meets the criteria, so the number to try is $101010$ .

Having never used a divisibility rule for 7 in my life before I was pleased when I checked my solution.

$101010 = 42 \times\ 2405$

Note that using the digits $1,2,4$ from the sequence generates the number 10101 which is divisible by 7 (and 3), but is not even.

Since the number consists of 1s and 0s, and is even number being divisible by 42, the last digit is 0. So the number can be written as 42×(5n)=21×(10n).
As the number is divisible by 21, we have to arrive at the smallest multiple of 10, consisting of 1s and 0s, which is divisible by 21.
10 = 10mod(21).
100 = 16mod(21).
1000 = 13mod(21).
10000 = 4mod(21).
100000= 19mod(21).
It can be seen that 10+13+19=42, a multiple of 21, so there is no need to search beyond 100,000, and the number is sum of 10+1000+100000=101010.

clearly, x must be a multiple of 5 42 = 210 I get 101010 = 42 2405 = 210*481

/ Open with C++ and ...there!! you have the solution. / // A trial and error code

include<iostream.h>

include<conio.h>

int digit(long x)
{ int digit=0; while(x!=0) { digit++;
x=x/10; } return digit; } int check_conditions(long x,int y) { int m;

for(int i=0;i<y;i++) { m=x%10; if(m!=0&&m!=1)
{ return 0;
} x=x/10; } return 1;
}

void main() { clrscr(); int x=0,d; long a=42;
while(x==0) { d=digit(a); x=check_conditions(a,d); if(x==0)
a+=42; }

cout<<"Atlast the answer is ..."<<a; getch(); }

//Sorry, i am unable to space it properly...

42=2 3 7

N is a number made of 0s and 1s that is divisible by 42

The test for 2 involves simply checking the last digit for divisibility by 2. In numbers involving only 1 and 0, this amounts to checking if the last digit is zero.

The tests for 3 and 9, exploit the decimal system such that you only have to add together all the digits in the number. For 3, the sum of the digits must be divisible by 3 for N to be; for 9, the sum must be divisible by 9. For example, 3∤176843∤17684 because 1+7+6+8+4=261+7+6+8+4=26, but 9∣176859∣17685 because 1+7+6+8+5=27=9⋅31+7+6+8+5=27=9⋅3. In 1-0 numbers, this amounts to counting all the ones.

And then, the smallest number that works for both is 1110

1110*7=7770

You can keep adding 7770 to 7770 until you get 101010 which is N

Here's a python script that is brute force, but simple to write:

def allOnesAndZeros(string):
    for c in string:
        if c != '1' and c != '0':
            return False
    return True

x = 42
while not allOnesAndZeros(str(x)):
    x = x + 42
print(x)

I'm not sure if this is cheating, but excel really does the heavy lifting on this one. The answer has to be a multiple of 5 to get a zero on the end, so I just put in 42* 5, 10 etc till I was over 1000, then checked 10 00 ÷ 5, and re-started from there, then did the same with 100 00 ÷ 5. No division laws needed - and the 7 one is a pain anyway

I cheated :P
λ> fake_binary = 1 : [y * 10 + x | y <- fake_binary, x <- [0,1]]
λ> find (\x -> mod x 42 == 0) $ take 100000 fake_binary
Just 101010

The simplest way to solve this is to consider powers of 10 and the resulting divisibility rules.

I was going to go about this as many other solutions did, but I came to the conclusion that doing $10^x\mod 42$ was clunky.

What we know: - The number only consists of 0 and 1. - 42 = 2 * 3 * 7

Hence, the number consisting of 1's and 0's must be a multiple of all of 42's factors.

• Divisibility by 2 : Ends in 1 :The number can't be divisible by 2, because all even (divisible by 2 ) numbers end in even (e.g. 0, 2, 4, 6, 8) digits.

Ends in 0: The number is divisible by 2;

• Divisibility by 3 : Rule for divisibility by 3 : the sum of the digits has to be divisible by 3 .

Assume there are X 1' s and Y 0's , because the Y's don't contribute to the sum, the only thing that matters is the number of 1's . Hence the number of 1's has to be a mulitple of 3 (e.g. 3, 6, 9, 12) .

• Divisibility by 7: This is slightly more tricky, and I solved this on a modulo basis. Also, moduli follow multiplicative rules. This helps because $x^n\mod a=((x\mod a)(x^{n-1}\mod a))\mod a$ and we can continue recursively. For example, $10^3\mod 7 = ((10\mod 7) * (10\mod 7) * (10\mod 7)) \mod 7$

$10^0\mod7=1$

$10^1\mod7=1*3\mod7=3$

$10^2\mod7=3*3\mod7=2$

$10^3\mod7=2*3\mod7=6$

$10^4\mod7=6*3\mod7=4$

$10^5\mod7=4*3\mod7=5$

$10^6\mod7=5*3\mod7=1$

Because we've wrapped back around to 1 , we've found all possible values for $10^x\mod7$ . The problem we're trying to solve is to add these powers above in such a way that the sum (which is also our number consisting of 1's and 0's ) is congruent to $0\mod 7$ .

Additionally, because we need to satisfy the divisibility by 3 , we can only add 3,6,9,12...3 * n terms.

Thankfully, we can reach such a sum by adding the 3 + 6 + 5 = 14 , which we know is divisible by 7 .

This means that we are adding numbers $10^1 + 10^3 + 10^5 = 101010$ .

I used the process of elimination.

We know that X is divisible by 3 and that the number only has 0's and 1's in it, which means that there have to be a multiple of 3 1's. We also know that it has to be even, if divisible by 2. That means that the first value to check for is 1110 then 10110, since that's the next lowest we can make and so on.

When we get to 11100 we realize that since we subtract the last digit twice to check for (mod 7), none of trailing 0's will matter. That of cause means that X needs to end in "...10", a "...00" ending would be similar to an already tried number.

That's how I got to 101010, not very elegant, but I'm not really a mathematician.

It would be fun to know if 1010100 is next and maybe something of the distribution of solution between 101010 and 10^100. Maybe I'll make a program some time to check.

These solutions seem all very complicated. I probably got lucky. The multiplier has to end in a 5 to turn the 2 into a 0. To turn the 40 into 1s and 0s you multiply by 25. Except you'll be carrying over a ten from the 2x5, so it needs to be 24. 245 didn't work so I stuck a zero in between the 24 and the 5 to make 2405. Remarkably, that multiplied by 42 came to 101,010.

Is it wrong that I used Excel? In column A, I entered 1. Then in cell A2 I entered =A1+1. Cell B1 was =A1*B1. For cell C1, I used =LEN(B1)-LEN(SUBSTITUTE(B1,"1",""))+LEN(B1)-LEN(SUBSTITUTE(B1,"0","")). Then for D1 I used =LEN(B1). Finally in Cell E1, I used =IF(C1=D1,"Yes","No"). Then I dragged the first row of formulas down a bunch. I used a little conditional formatting to highlight when a Cell in Column E was "Yes" to make it easier to find.

LOL, who can write the best script to solve brute force? Here's Perl:

$decimal = 1;
do { $redecimal = sprintf "%b", $decimal++ } # print as binary, interpret as decimal
  while ($redecimal % 42);
print "Founit: $redecimal\n";

I've written a python script to do the 'trial and error' component of this. You could write a script that just tries each number until it satisfies the requirements of both being a number that contains just 0's and 1's and is divisible by 42, but may take many days and the script below uses the hints provided in the question. If you're wanting to get into programming, I couldn't recommend it highly enough. The script below took less than a second to execute, although a good part of an hour to write!

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

"""
This script is a simple script to obtain the answer of a brilliant.org question that is as follows:
'The positive number  is divisible by 42, and is composed of only 1s and 0s when written in base 10. What's the smallest number that  might be?'
The clue provided doesn't seem too useful until you realise the following:
42 is equal to 2*3*7:
Therefore, for a number to be divisible by 42 it must also be divisible by 2, 3 and 7.
According to the hint: 
* A number is only divisible by 2 if the last digit of is 2, 4, 6, 8, or 0.
* A number is only divisible by 3 if the sum of digits of is a multiple of 3.
* A number is only divisible by 7 if subtracting twice the last digit of from the remaining digits gives a multiple of 7. 
We can then run through the permutations of the numbers containing the digits 0 and 1 to get our answer.
"""

# Import the itertools function.
from itertools import combinations_with_replacement

""" Create two functions that we will use to determine if our answer is right  """

def is_divisible_by_three(number):
    if sum(int(digit) for digit in str(combination)) % 3 == 0:
        return True
    else:
        return False

def is_divisible_by_seven(number):
    if len(str(number)) <= 2:
        if number % 7 == 0:
            return True
        else:
            return False
    else:
          new_number = int(''.join(str(combination)[:-1]))-2*int(str(combination)[:-1]))
          return is_divisible_by_seven(new_number)

""" Initialisation step
We know that we start with a 1 and end with a 0. We just don't know the combination of 0 and 1s in-between.
We initilise n, the number of 0 and 1s in between as 1 and increment this number by 1 each iteration.
Therefore the first iteration will check the numbers: 100 and 110
The following iteration will check the numbers 1000, 1010, 1100 and 1110 etc.
After a while, it makes sense to let the computer to do the work for us as the number of combinations is proportional to n!
"""

n=1

while True:  # An infinite while loop 
    # A complicated one-liner that provides us with all of the combinations of 0 and 1 for a given n.
    # If n is 4, this list will go from 100000 to 111110
    combinations = [int("1" + midfix + "0") 
            for midfix in sorted(list(set([''.join(list(combination)) 
                for combination in combinations_with_replacement(''.join([str(num) for num in [0,1]*n]), n)])))]
    # For each combination check if it is divisible by 3, only keep those that are divisible by 3:
    combinations = [combination 
            for combination in combinations
                if is_divisible_by_three(number)]

    # For each combination check if it is divisibly by 7, only keep those that are divisible by 7
    combinations = [combination
            for combination in combinations
                if is_divisible_by_seven(number)]

    # Do we have anything left.
    if len(combinations) > 0:
        print(combinations)
        # Yes! Now break from loop
        break
    else:  # Continue with next iteration
        n += 1

And within a second we have our answer!

In binary, the numbers ( $n$ ) are replaced for ones and zeros. The smallest decimal number divisible by 42 is 42, and the smallest binary number divisible by 42 is the binary number of 42: $101010$

In order for X to be divisible by 42, it must be divisible by 2, 3 and 7 (42 = 2 3 7). Therefore, the last digit must be 0, otherwise it would not be divisible by 2. Now, what I did was I tested 2 cases: last 2 digits are 10 or last 2 digits are 00. Case 1: Using the divisibility rule for 3, we know there should be at least 3 1s. We also know that subtracting twice the last digit from the remaining number until we are left with a simple number must result in a multiple of 7. Using what we have so far, 10, we notice the digit resulting is -2, assuming the number continues on. Through some analysis, I was able to obtain 101010.

Case 2: Since there are 2 0s, the resulting number X would be longer (Since it still requires 3 1s).

Side note: I could have used modular arithmetics, but I was feeling a bit lazy.

A quick program that took a minute to write that solves it the plug n' chug way - it would work with any number input or any specific digit requirement

http://www.codeskulptor.org/#user43 EX2YEkKNYz 2.py

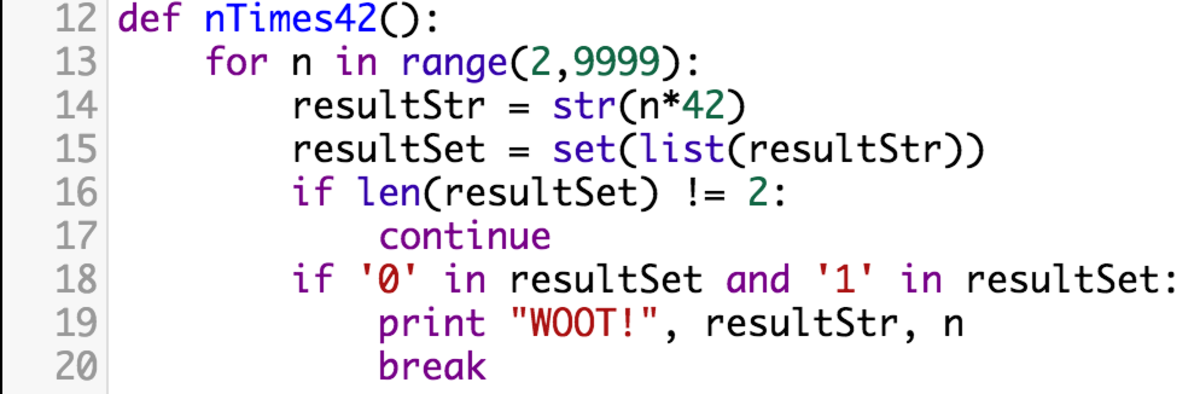
Just wrote a Python script.

There is an Easy solution: 42=7x6 So first find a number that is divisible by 7, consists of only 0, 1. Okay, 1001 is divisible but it sum of the digits is 2. so if we line up like 1001100110010 then it will be divisible by 42. But from the sense you can tell it is not a possible solution. Again 10101 is divisible by 7, and sum of the digits are 3!!! Hurray we got the number! To make it divisible by 42 just add 0. So the answer is 101010!!!! Just by inspection!