26 of 100: Triple Absolute

Notice that $y=| \ {\color{#D61F06}|} \ \underbrace{|x-10|+10}_{\text{always positive}} \ {\color{#D61F06}|} \ -10|+10=||x-10|+10-10|+10={\color{#D61F06}|}\ \underbrace{|x-10|}_{\text{non-negative}}\ {\color{#D61F06}|} \ +10=|x-10|+10$ Thus $y=|x-10|+10$ and $y-10=|x-10| \ge 0$ and $y \ge 10$ . Also, $y=10$ occurs when $|x-10|=0$ , or $x=10$ .

Therefore, $y$ indeed can take its minimum value as $10$ for $x=10$ .

Important point to note is that the lower bound of an absolute value function(definition) is zero.So when we plug in $x=10$ we get the least value. Therefore the least value of $y=\Huge|\huge|\large|x-10\large|+10\huge|$ $-10\Huge|$ $+10=0+10=\boxed {10}.$

By graphing this we can see that the (x,y) = (10,10) is our min point so the lowest y-value is 10. 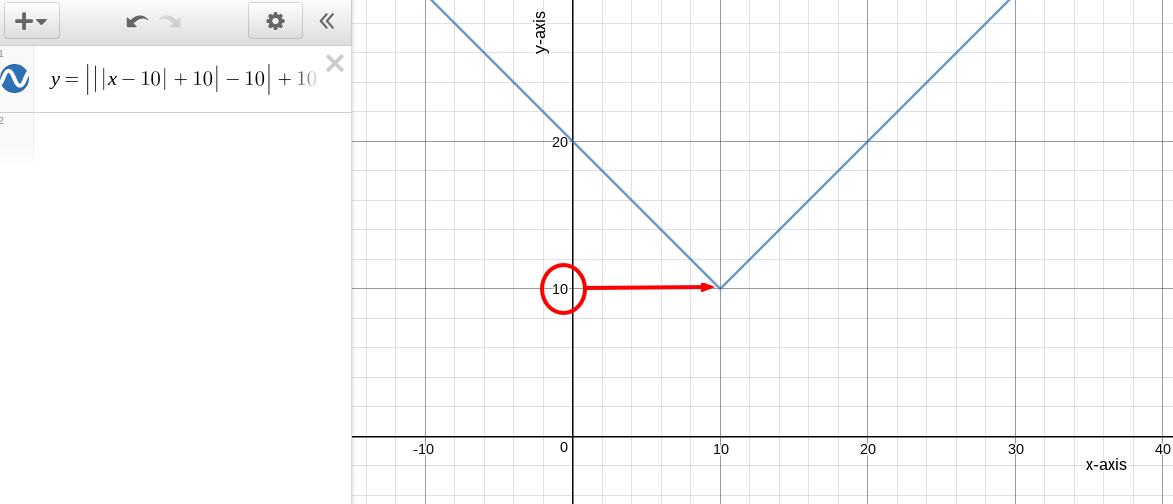Link to this DESMOS graph

$\large{\color{#69047E}{y} =} \Huge| \huge| \Large| \large{\color{#3D99F6}{x} - \color{#D61F06}{10}} \Large| \large{+ \color{#D61F06}{10}} \huge| \large{- \color{#D61F06}{10}} \Huge| \large{+ \color{#D61F06}{10}} = \huge| \Large| \large{\color{#3D99F6}{x} - \color{#D61F06}{10}} \Large| \large{+ \color{#D61F06}{10}} \large{- \color{#D61F06}{10}} \huge| \large{+ \color{#D61F06}{10}} = \Large| \large{\color{#3D99F6}{x} - \color{#D61F06}{10}} \Large| \large{+ \color{#D61F06}{10}}$

Thus, $y \geq 10$ with equality when $x=10$ , and hence the solution is $\boxed{y = 10}$ .

There are several good pure solutions elsewhere. This is test taker eye view. The only mystery is how this thing, as composed, rates three cacti. Since | <anything> | cannot be negative and positive 10 is added to that, three of the answers, 0,-10, < -10 are immediately out. It is also apparent the minimum possible value for y is 10. That leaves only the question of 10 or 20. So if there is any way to get the quantity in absolute value to 0 then y = 10 is the answer. It is not difficult to see that x = 10 leaves 10 -10 = 0 inside the absolute value achieving the absolute minimum y = 10.

Logically, the smallest an expression in absolute value can be is 0. Since absolute value works a bit like parentheses, we work inside out. The only one we can really control is the first, innermost expression. Let that be equal to 0. Then continue calculating until you find y.

If we let x=10, then the value of the nested absolute value expression is 0, and y=0+10=10. Since we can't have an absolute value less than zero, 10 is the minimum value of the whole expression on the right side of the equation.

|||x-10|+10|-10| cannot be negative. The minimum is 0. 0+10 is 10 so the smallest y=10

Because there are absolute value signs the smallest integer available is 0. So by making x=10 you get 10-10=0 then 0+10=10 then 10-10=0 then y=0+10

The final answer is y=10

We know that any mod value is non negative real no,i.e. |something| is non negative.
So the least value inside the mod is 0
Hence, minimum value of (y=10)

If $x-10=n≤-1$ , then because it is the absolute value of n, n will be positive. The least value we can get $n$ to be is $0$ . To do this, x has to equal what is is being subtracted by, which is $10$ . So, $10-10+10-10+10$ in absolute value equals $**10**$ .

Lol lmao keep laughing

Working backwards, we want |||x-10|+10|-10| to be as small as possible (notice I didn't include the plus ten at the end) so the smallest number this could be is 0 because absolute value stops us from having any negatives, so then we want |||x-10|+10| to be 10, meaning |x-10|+10 = -10 or 10. it couldn't be -10 because |x-10| never would equal -20, but 10 is possible, IF |x-10| = 0, and simply we just have to use x as ten in there, so this concludes the proof that y=10 (the lowest number - look to the beginning of my proof) IS possible, and that is therefore the answer

I used simple logic of absolute functions

i.e., x < 10

x = 10

x > 10

So we will look into all three cases and whichever gives least result, thats the result

CASE 1:

x > 10

y = | | | x - 10 | + 10 | - 10 | + 10

= | | x - 10 + 10 | - 10 | + 10

= | | x | - 10 | + 10

= | x - 10 | + 10

= x - 10 + 10

y = x [ x > 10, so y > 10 ]

CASE 2:

x < 10

y = | | | x - 10 | + 10 | - 10 | + 10

= | | -(x - 10) + 10 | - 10 | + 10

= | | - x + 20 | - 10 | + 10

= | - x + 20 - 10 | + 10

= - x + 10 + 10

y = - x + 20 [ x < 10, so y > 10 ]

CASE 3:

x = 10 , which follows the same steps as case 1, so we have to just replace x by 10 in case 1

By case 1, y = x = 10, which is the least value in all of the three cases possible for absolute function.

Hence answer is y = 10

There is a +10 at the end of the function, and rest of the function is an absolute value, so the minimum of the function greater than or equal to 10. If a value of can be plugged in to make the absolute value equal zero, x=10, then the function's minimum must be 10.

Besides graphing the expression we have, we can also solve it by using the mentioned advice. We know the domain of our expression is all real numbers so by plugging few values for $x$ , we notice the least value for $y$ is $10$ , and the range is $(10, \infty)$